MultinomialDistribution[n,{p1,p2,…,pm}]
represents a multinomial distribution with n trials and probabilities pi.


MultinomialDistribution
MultinomialDistribution[n,{p1,p2,…,pm}]
represents a multinomial distribution with n trials and probabilities pi.
Details
- The probability for a vector
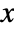 of non-negative integers
of non-negative integers 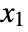 ,
, 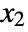 , …,
, …, 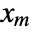 in a multinomial distribution is
in a multinomial distribution is 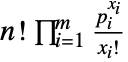 .
. - The number of trials n can be any positive integer, and
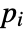 can be any non-negative real numbers such that
can be any non-negative real numbers such that 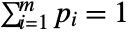 .
. - MultinomialDistribution allows n and pi to be dimensionless quantities. »
- MultinomialDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- MultinomialDistribution[n,{p1,p2,…,pm}] represents a discrete multivariate statistical distribution supported over the subset of
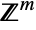 consisting of all tuples
consisting of all tuples 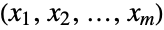 of integers satisfying
of integers satisfying 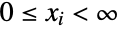 and
and 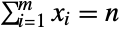 and characterized by the property that each of the
and characterized by the property that each of the 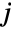
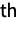 (univariate) marginal distributions has a BinomialDistribution for
(univariate) marginal distributions has a BinomialDistribution for 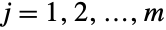 . In other words, each of the variables
. In other words, each of the variables 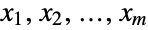 satisfies xjBinomialDistribution[n,pj] for
satisfies xjBinomialDistribution[n,pj] for 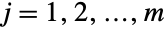 . The multinomial distribution is parametrized by a positive integer n and a vector {p1,p2,…,pm} of non-negative real numbers satisfying
. The multinomial distribution is parametrized by a positive integer n and a vector {p1,p2,…,pm} of non-negative real numbers satisfying 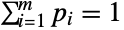 , which together define the associated mean, variance, and covariance of the distribution.
, which together define the associated mean, variance, and covariance of the distribution. - The multinomial distribution models a scenario in which n draws are made with replacement from a collection with type i representing pi percent of the total population. This can be visualized as an urn model in which n balls are drawn with replacement from an urn containing m different types of balls with the condition that the percentage of balls of type i is pi balls for
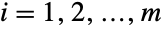 . The multinomial distribution was first analyzed in a 1708 essay by French mathematician Pierre Raymond de Montmort, making it one of the earliest studied multivariate probability distributions. It has since become a tool in the study of a number of different phenomena, including kinetic theory in particle physics and overstatement in accounting. It is also widely used in the analysis of contingency tables, telecommunications modeling, medical epidemiology, and photon counting.
. The multinomial distribution was first analyzed in a 1708 essay by French mathematician Pierre Raymond de Montmort, making it one of the earliest studied multivariate probability distributions. It has since become a tool in the study of a number of different phenomena, including kinetic theory in particle physics and overstatement in accounting. It is also widely used in the analysis of contingency tables, telecommunications modeling, medical epidemiology, and photon counting. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a multinomial distribution. Distributed[x,MultinomialDistribution[n,{p1,p2,…,pm}]] , written more concisely as xMultinomialDistribution[n,{p1,p2,…,pm}], can be used to assert that a random variable x is distributed according to a multinomial distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for multinomial distributions may be given using PDF[MultinomialDistribution[n,{p1,p2,…,pm}]] and CDF[MultinomialDistribution[n,{p1,p2,…,pm}]]. The mean, median, variance, covariance, raw moments, and central moments may be computed using Mean, Median, Variance, Covariance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a multinomial distribution, EstimatedDistribution to estimate a multinomial parametric distribution from given data, and FindDistributionParameters to fit data to a multinomial distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic multinomial distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic multinomial distribution.
- TransformedDistribution can be used to represent a transformed multinomial distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a multinomial distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving multinomial distributions.
- MultinomialDistribution is related to a number of other distributions. MultinomialDistribution is connected to the BinomialDistribution as discussed above and, while the one-dimensional marginal PDFs of the MultinomialDistribution each have a BinomialDistribution, the multivariate marginals do not simplify to named distributions. The urn model for MultinomialDistribution is related to that of MultivariateHypergeometricDistribution in the sense that the latter distribution models drawing without replacement. Because of its relation to the univariate BinomialDistribution, it is also related to BernoulliDistribution, NormalDistribution, PoissonDistribution, BetaBinomialDistribution, and NegativeBinomialDistribution.
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom vectors from a multinomial distribution:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
The univariate marginals follow BinomialDistribution:
Multivariate marginals do not simplify:
Plot the probability density function of the marginal for fixed values of parameters:
Use dimensionless Quantity to define MultinomialDistribution:
Applications (5)
There are two candidates in an election where the winner is chosen based on a simple majority. Each of ![]() voters votes for candidate 1 with probability
voters votes for candidate 1 with probability ![]() and for candidate 2 with probability
and for candidate 2 with probability ![]() , where
, where ![]() , so that a voter may choose not to vote for either candidate. When
, so that a voter may choose not to vote for either candidate. When ![]() ,
, ![]() , the probability of one swing vote is:
, the probability of one swing vote is:
Probability that a winner won by one vote:
Probability that candidate 1 wins the election:
Probable outcome of the next election:
Average outcome of an election:
Distribute 5 balls among 3 containers, picking each container with equal probability. Find the probability that no container is empty:
Compute the same probability using SurvivalFunction:
Distribute ![]() balls among
balls among ![]() containers with equal probability. Find the probability that no container is empty for different values of
containers with equal probability. Find the probability that no container is empty for different values of ![]() and
and ![]() :
:
In calling a customer service center, one of three things may happen: the line is busy with probability 0.4, a caller gets the wrong party with probability 0.1, or a caller gets connected to an agent. Find the probability that a caller calling at 6 different times gets a busy signal 4 times and twice connects directly to an agent:
Find the probability that calling at 6 different times, a caller gets the wrong party at least twice:
Simulate 6 calling attempts done at different times:
In a certain city, out of all 911 calls 30% were requesting an ambulance, 15% were requesting the fire department, and the rest were police requests. Find the probability that in the next 10 emergency calls, 2 will ask for an ambulance, 1 for the fire department, and 7 for police:
Simulate the request distribution for the next 100 calls:
Define a multivariate Pólya distribution as a parameter mixture of negative multinomial distribution:
Properties & Relations (3)
Relationships to other distributions:
A bivariate multinomial distribution is a BinomialDistribution:
A univariate multinomial distribution is a shifted BernoulliDistribution:
Possible Issues (2)
MultinomialDistribution is not defined when n is not a positive integer:
MultinomialDistribution is not defined when the elements of p do not sum to 1:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Related Guides
Text
Wolfram Research (2010), MultinomialDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MultinomialDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "MultinomialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MultinomialDistribution.html.
APA
Wolfram Language. (2010). MultinomialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MultinomialDistribution.html
BibTeX
@misc{reference.wolfram_2025_multinomialdistribution, author="Wolfram Research", title="{MultinomialDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MultinomialDistribution.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_multinomialdistribution, organization={Wolfram Research}, title={MultinomialDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MultinomialDistribution.html}, note=[Accessed: 28-February-2026]}