MultivariateHypergeometricDistribution

MultivariateHypergeometricDistribution[n,{m1,m2,…,mk}]

represents a multivariate hypergeometric distribution with n draws without replacement from a collection containing mi objects of type i.

Details

  • The probability for a vector 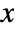of non-negative integers 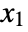, , 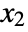…, 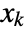in a multinomial distribution is proportional to product_(i=1)^kTemplateBox[{{m, _, i}, {x, _, i}}, Binomial] given that .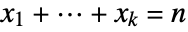
  • The numbers mi can be any non-negative integers and n any positive integer less than or equal to m1+⋯+mk.
  • The number of trials n can be any positive integer and mi any non-negative integer.
  • MultivariateHypergeometricDistribution can be used with such functions as Mean, CDF, and RandomVariate.

Background & Context

  • MultivariateHypergeometricDistribution[n,{m1,m2,…,mk}] represents a discrete multivariate statistical distribution supported over the subset of 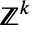consisting of all tuples 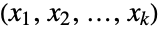of integers satisfying 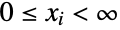and 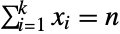and characterized by the property that each of the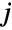 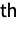^(th) (univariate) marginal distributions is a HypergeometricDistribution for 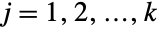. In other words, each of the variables 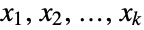satisfies xjHypergeometricDistribution[n,mj,m1+⋯+mk] for 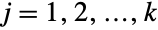. The multivariate hypergeometric distribution is parametrized by a positive integer n and by a vector {m1,m2,…,mk} of non-negative integers that together define the associated mean, variance, and covariance of the distribution.
  • The multivariate hypergeometric distribution models a scenario in which n draws are made without replacement from a collection containing mi objects of type i. This can be visualized as an urn model in which n balls are drawn without replacement from an urn containing k different types of balls, with the condition that there are mi balls of type i for 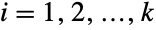. The multivariate hypergeometric distribution was first analyzed in a 1708 essay by French mathematician Pierre Raymond de Montmort, making it one of the earliest studied multivariate probability distributions. It has since become a tool in the study of a number of different phenomena, including faulty inspection procedures, and is a widely utilized model in fields such as statistical decision theory.
  • RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a multivariate hypergeometric distribution. Distributed[x,MultivariateHypergeometricDistribution[n,{m1,m2,…,mk}]] , written more concisely as xMultivariateHypergeometricDistribution[n,{m1,m2,…,mk}], can be used to assert that a random variable x is distributed according to a multivariate hypergeometric distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
  • The probability density and cumulative distribution functions for multivariate hypergeometric distributions may be given using PDF[MultivariateHypergeometricDistribution[n,{m1,m2,…,mk}]] and CDF[MultivariateHypergeometricDistribution[n,{m1,m2,…,mk}]]. The mean, median, variance, covariance, raw moments, and central moments may be computed using Mean, Median, Variance, Covariance, Moment, and CentralMoment, respectively.
  • DistributionFitTest can be used to test if a given dataset is consistent with a multivariate hypergeometric distribution, EstimatedDistribution to estimate a multivariate hypergeometric parametric distribution from given data, and FindDistributionParameters to fit data to a multivariate hypergeometric distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic multivariate hypergeometric distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic multivariate hypergeometric distribution.
  • TransformedDistribution can be used to represent a transformed multivariate hypergeometric distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a multivariate hypergeometric distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving multivariate hypergeometric distributions.
  • MultivariateHypergeometricDistribution is related to a number of other distributions. It is connected to HypergeometricDistribution as discussed above, and while the one-dimensional marginal PDFs of MultivariateHypergeometricDistribution are each a HypergeometricDistribution, the multivariate marginals do not simplify to named distributions. The urn model for MultivariateHypergeometricDistribution is related to that of MultinomialDistribution, in the sense that the latter distribution models drawing with replacement. Because of its relation to the univariate HypergeometricDistribution, MultivariateHypergeometricDistribution is also related to GeometricDistribution, NormalDistribution, PoissonDistribution, PearsonDistribution, and BetaBinomialDistribution.

Examples

open allclose all

Basic Examples  (4)

Probability mass function:

Cumulative distribution function:

Mean and variance:

Covariance:

Scope  (7)

Generate a sample of pseudorandom vectors from a multivariate hypergeometric distribution:

Compare sample histogram to the PDF of the multivariate hypergeometric distribution:

Distribution parameters estimation:

Estimate the distribution parameters from sample data:

Goodness-of-fit test:

Skewness:

The distribution becomes symmetric with an equal number of objects:

Kurtosis:

In the limit it behaves like a binormal distribution:

Correlation:

Hazard function:

Marginals do not simplify to known distributions:

Applications  (1)

An urn contains 12 red balls, 23 blue balls, and 9 green balls. Find the distribution of a sample of 5 balls drawn without replacement:

Find the probability of exactly 2 red balls and 3 green balls in the sample:

Find the average number of balls of each color in a sample:

Simulate the composition of 30 samples:

Visualize the samples:

Properties & Relations  (2)

Relationships to other distributions:

Bivariate hypergeometric distribution is equivalent to HypergeometricDistribution:

Wolfram Research (2010), MultivariateHypergeometricDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MultivariateHypergeometricDistribution.html.

Text

Wolfram Research (2010), MultivariateHypergeometricDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MultivariateHypergeometricDistribution.html.

CMS

Wolfram Language. 2010. "MultivariateHypergeometricDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MultivariateHypergeometricDistribution.html.

APA

Wolfram Language. (2010). MultivariateHypergeometricDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MultivariateHypergeometricDistribution.html

BibTeX

@misc{reference.wolfram_2024_multivariatehypergeometricdistribution, author="Wolfram Research", title="{MultivariateHypergeometricDistribution}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/MultivariateHypergeometricDistribution.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_multivariatehypergeometricdistribution, organization={Wolfram Research}, title={MultivariateHypergeometricDistribution}, year={2010}, url={https://reference.wolfram.com/language/ref/MultivariateHypergeometricDistribution.html}, note=[Accessed: 21-December-2024 ]}