HypergeometricDistribution

HypergeometricDistribution[n,nsucc,ntot]

represents a hypergeometric distribution.

Details

Background & Context

  • HypergeometricDistribution[n,nsucc,ntot] represents a discrete statistical distribution defined for integer values 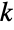contained in 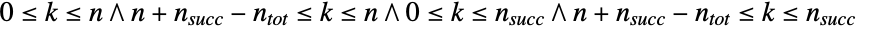and determined by the integer parameters n, nsucc, and ntot that satisfy 0<n≤ntot and 0≤nsucc≤ntot and that represent the number of draws of the experiment, the number of successes within that population, and the size of the population drawn from, respectively. The hypergeometric distribution has a probability density function (PDF) that is discrete and unimodal. The distribution is sometimes also referred to as the central or classic hypergeometric distribution to differentiate it from the related and qualitatively-similar distributions of Wallenius (WalleniusHypergeometricDistribution) and Fisher (FisherHypergeometricDistribution).
  • The hypergeometric distribution gives the distribution of the number of successes in n draws (without replacement) from a population of size ntot containing nsucc successes and can be visualized as an urn model whereby n balls are drawn without replacement from an urn containing nsucc blue balls and ntot-nsucc green balls. The hypergeometric distribution dates back to the 1710s work of de Moivre, who obtained it as a solution to an urn problem proposed even earlier by Huygens and related to the urn problem described above. The name of the hypergeometric distribution derives from the fact that its PDF can be expressed in terms of the generalized hypergeometric function (Hypergeometric2F1), and the distribution itself is used to model a number of quantities across various fields. In particular, the hypergeometric distribution has been used as a tool in the study of queueing models, manufacturing systems, population dynamics, contingency table analysis, and quantum cryptography.
  • RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a hypergeometric distribution. Distributed[x,HypergeometricDistribution[n,nsucc,ntot]], written more concisely as xHypergeometricDistribution[n,nsucc,ntot], can be used to assert that a random variable x is distributed according to a hypergeometric distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
  • The probability density and cumulative distribution functions may be given using PDF[HypergeometricDistribution[n,nsucc,ntot],x] and CDF[HypergeometricDistribution[n,nsucc,ntot],x], though one should note that there is no closed-form expression for its PDF. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
  • DistributionFitTest can be used to test if a given dataset is consistent with a hypergeometric distribution, EstimatedDistribution to estimate a hypergeometric parametric distribution from given data, and FindDistributionParameters to fit data to a hypergeometric distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic hypergeometric distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic hypergeometric distribution.
  • TransformedDistribution can be used to represent a transformed hypergeometric distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a hypergeometric distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving hypergeometric distributions.
  • HypergeometricDistribution is related to a number of other statistical distributions. For example, HypergeometricDistribution is generalized by both FisherHypergeometricDistribution and WalleniusHypergeometricDistribution in the sense that HypergeometricDistribution[n,nsucc,ntot] has the same PDF as both FisherHypergeometricDistribution[n,nsucc,ntot,1] and WalleniusHypergeometricDistribution[n,nsucc,ntot,1]. As 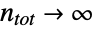, HypergeometricDistribution limits to BinomialDistribution, and MultivariateHypergeometricDistribution is an obvious higher-dimensional generalization of HypergeometricDistribution. HypergeometricDistribution is also related to GeometricDistribution, NormalDistribution, PoissonDistribution, PearsonDistribution, and BetaBinomialDistribution.

Examples

open allclose all

Basic Examples  (3)

Probability mass function:

Cumulative distribution function:

Mean and variance:

Scope  (7)

Generate a sample of pseudorandom numbers from a hypergeometric distribution:

Compare its histogram to the PDF:

Distribution parameters estimation:

Estimate the distribution parameters from sample data:

Compare the density histogram of the sample with the PDF of the estimated distribution:

Skewness:

Kurtosis:

Different moments with closed forms as functions of parameters:

Moment:

CentralMoment:

FactorialMoment:

Closed form for symbolic order:

Cumulant:

Hazard function:

Quantile function:

Applications  (6)

CDF of HypergeometricDistribution is an example of a right-continuous function:

Suppose an urn has 100 elements, of which 40 are special:

The probability density function for a draw of 50 elements:

The probability distribution that there are 20 special elements in a draw of 50 elements:

Compute the probability that there are more than 25 special elements in a draw of 50 elements:

Compute the expected number of special elements in a draw of 50 elements:

Suppose there are 5 defective items in a batch of 10 items, and 6 items are selected for testing. Simulate the process of testing when the number of defective items found is counted:

Find the probability that there are 2 defective items in the sample:

Find the distribution of the number of spades in a five-card poker hand:

Find the probability that there are at least 2 spades in the poker hand:

A lottery sells 10 tickets for $1 per ticket. Each time there is only one winning ticket. A gambler has $5 to spend. Find his probability of winning if he buys 5 tickets in 5 different lotteries:

His probability of winning is greater if he buys 5 tickets in the same lottery:

An urn contains white balls and 1 blue ball. Two players draw balls from the urn without replacement until the blue ball is drawn. The player who draws the blue ball wins. Find the chance of winning for the player who draws the first ball. Assuming the first player wins at the draw, the probability that the previous draws were all white follows HypergeometricDistribution:

The conditional probability of drawing a blue ball given that the previous balls were white:

The resulting probability is a sum over :

When the number of white balls is odd, both players have an equal chance of winning:

When the number of white balls is even, the game is unfair:

Properties & Relations  (8)

The probability of getting an irrational number or negative number is zero:

The characteristic function of the hypergeometric distribution is defined in terms of Hypergeometric2F1:

Relationships to other distributions:

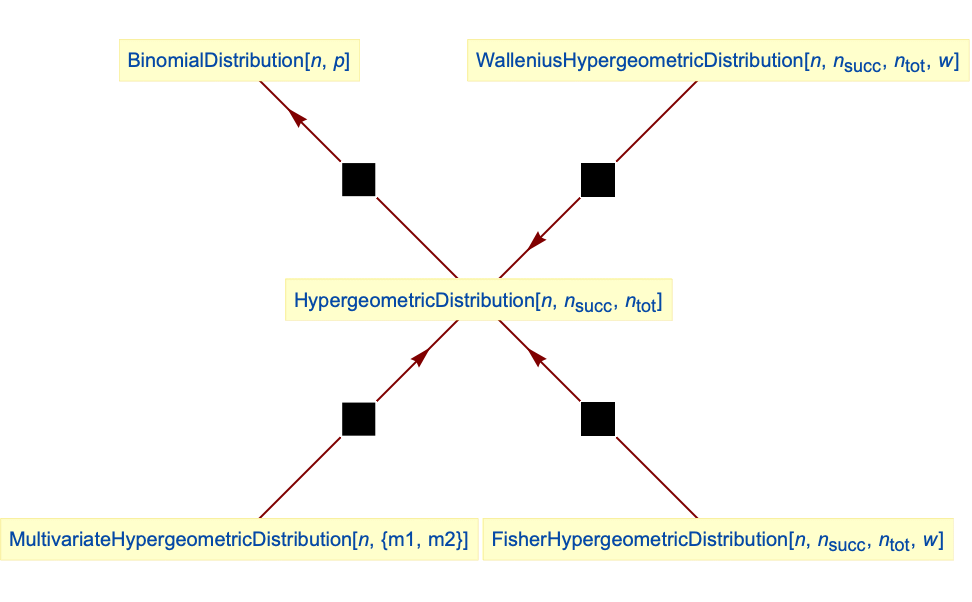
The infinite population limit of HypergeometricDistribution is BinomialDistribution:

Hypergeometric distribution is a special case of FisherHypergeometricDistribution:

Hypergeometric distribution is a special case of WalleniusHypergeometricDistribution:

Hypergeometric distribution is equivalent to a bivariate MultivariateHypergeometricDistribution:

HypergeometricDistribution can be obtained from two independent binomial variates conditioning of their total:

Possible Issues  (4)

HypergeometricDistribution is not defined when ntot, nsucc, or n is non-positive:

HypergeometricDistribution is not defined when n>ntot:

HypergeometricDistribution is not defined when nsucc>ntot:

Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:

Wolfram Research (2007), HypergeometricDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/HypergeometricDistribution.html.

Text

Wolfram Research (2007), HypergeometricDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/HypergeometricDistribution.html.

CMS

Wolfram Language. 2007. "HypergeometricDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HypergeometricDistribution.html.

APA

Wolfram Language. (2007). HypergeometricDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HypergeometricDistribution.html

BibTeX

@misc{reference.wolfram_2024_hypergeometricdistribution, author="Wolfram Research", title="{HypergeometricDistribution}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/HypergeometricDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hypergeometricdistribution, organization={Wolfram Research}, title={HypergeometricDistribution}, year={2007}, url={https://reference.wolfram.com/language/ref/HypergeometricDistribution.html}, note=[Accessed: 21-November-2024 ]}