PolyaAeppliDistribution

PolyaAeppliDistribution[θ,p]

represents a Pólya–Aeppli distribution with shape parameters θ and p.

Details

  • The Pólya–Aeppli distribution is a compound geometric Poisson distribution, i.e. the distribution of a sum of independent identically distributed geometric random variates where the number of variates follows Poisson distribution.
  • The probability for positive integer value 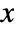in a Pólya–Aeppli distribution is proportional to p^(x-1) TemplateBox[{{1, -, x}, 2, {-, {{(, {{(, {1, -, p}, )}, , theta}, )}, /, p}}}, Hypergeometric1F1].
  • PolyaAeppliDistribution allows θ to be any positive real number, and p is a number between 0 and 1.
  • PolyaAeppliDistribution allows θ and p to be a dimensionless quantity. »
  • PolyaAeppliDistribution can be used with such functions as Mean, CDF, and RandomVariate.

Background & Context

  • PolyaAeppliDistribution[θ,p] represents a discrete statistical distribution defined for integer values 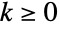and determined by the positive real parameters θ and p (called "shape parameters"), where 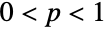. The Pólya–Aeppli distribution has a probability density function (PDF) that is discrete and unimodal and whose overall shape (its height, its spread, and the horizontal location of its maximum) is determined by the values of θ and p. The Pólya–Aeppli distribution is sometimes referred to as the geometric Poisson distribution, though it should not be confused with either the geometric (GeometricDistribution) or Poisson (PoissonDistribution) distributions.
  • The Pólya–Aeppli distribution dates back to the dissertation work of Swiss mathematician Alfred Aeppli and the subsequent investigations of Aeppli's adviser George Pólya throughout the 1920s and 1930s. Classically, the Pólya–Aeppli distribution is the distribution of a sum of independent identically distributed geometric (GeometricDistribution) random variates where the number of variates follows a Poisson distribution (PoissonDistribution), and in particular, the distribution can be described as an urn model in which the number of urns is Poisson distributed, while the number of marbles in each urn follows a geometric distribution. Since its inception, the Pólya–Aeppli distribution has been used in biometrics and in the study of Markov models, as well as in the modeling of phenomena in fields like biology, queueing theory, accident statistics, and bioinformatics.
  • RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Pólya–Aeppli distribution. Distributed[x,PolyaAeppliDistribution[θ,p]], written more concisely as xPolyaAeppliDistribution[θ,p], can be used to assert that a random variable x is distributed according to a Pólya–Aeppli distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
  • The probability density and cumulative distribution functions may be given using PDF[PolyaAeppliDistribution[θ,p],x] and CDF[PolyaAeppliDistribution[θ,p],x], though one should note that there is no closed-form expression for its PDF. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
  • DistributionFitTest can be used to test if a given dataset is consistent with a Pólya–Aeppli distribution, EstimatedDistribution to estimate a Pólya–Aeppli parametric distribution from given data, and FindDistributionParameters to fit data to a Pólya–Aeppli distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Pólya–Aeppli distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Pólya–Aeppli distribution.
  • TransformedDistribution can be used to represent a transformed Pólya–Aeppli distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Pólya–Aeppli distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Pólya–Aeppli distributions.
  • PolyaAeppliDistribution is related to a number of other statistical distributions. It has PoissonDistribution as a limiting case in the sense that the limit of the PDF of PolyaAeppliDistribution[θ,p] as p→0 (for 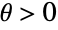) is precisely equivalent to the PDF of PoissonDistribution[θ]. PolyaAeppliDistribution is also closely related to GeometricDistribution, PoissonConsulDistribution, SkellamDistribution, and CompoundPoissonDistribution.

Examples

open allclose all

Basic Examples  (3)

Probability mass function:

Cumulative distribution function:

Mean and variance:

Scope  (8)

Generate a sample of pseudorandom numbers from a Pólya–Aeppli distribution:

Compare its histogram to the PDF:

Distribution parameters estimation:

Estimate the distribution parameters from sample data:

Compare a density histogram of the sample with the PDF of the estimated distribution:

Skewness:

Limiting values:

Kurtosis:

Limiting values:

Different moments with closed forms as functions of parameters:

Moment:

CentralMoment:

FactorialMoment:

Closed form for symbolic order:

Cumulant:

Hazard function:

Quantile function:

Use dimensionless Quantity to define PolyaAeppliDistribution:

Applications  (2)

The CDF of PolyaAeppliDistribution is an example of a right-continuous function:

The number of hotbeds of a contagious disease follows PoissonDistribution with mean 10, while the number of sick people within the hotbed follows GeometricDistribution with mean 7. Find the probability that the total number of sick people is greater than 70:

Plot the distribution mass function for the number of sick people:

Properties & Relations  (3)

Pólya–Aeppli distribution is closed under addition:

Proof using characteristic functions:

Relationships to other distributions:

PoissonDistribution is a limiting case for Pólya–Aeppli distribution:

Wolfram Research (2010), PolyaAeppliDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/PolyaAeppliDistribution.html (updated 2016).

Text

Wolfram Research (2010), PolyaAeppliDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/PolyaAeppliDistribution.html (updated 2016).

CMS

Wolfram Language. 2010. "PolyaAeppliDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/PolyaAeppliDistribution.html.

APA

Wolfram Language. (2010). PolyaAeppliDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PolyaAeppliDistribution.html

BibTeX

@misc{reference.wolfram_2024_polyaaepplidistribution, author="Wolfram Research", title="{PolyaAeppliDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/PolyaAeppliDistribution.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_polyaaepplidistribution, organization={Wolfram Research}, title={PolyaAeppliDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/PolyaAeppliDistribution.html}, note=[Accessed: 21-December-2024 ]}