represents a logarithmic series distribution with parameter θ.


LogSeriesDistribution
represents a logarithmic series distribution with parameter θ.
Details
- LogSeriesDistribution is also known as the logarithmic distribution.
- The probability for value
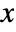 in a logarithmic series distribution is
in a logarithmic series distribution is 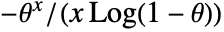 for positive integers, and is zero otherwise. »
for positive integers, and is zero otherwise. » - LogSeriesDistribution allows θ to be any real number between 0 and 1.
- LogSeriesDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- LogSeriesDistribution[θ] represents a discrete statistical distribution defined for integer values
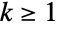 determined by the real parameter θ for which
determined by the real parameter θ for which 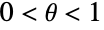 . The logarithmic series distribution has a probability density function (PDF) that is discrete and monotone decreasing. It is sometimes referred to as the log-series distribution or logarithmic distribution.
. The logarithmic series distribution has a probability density function (PDF) that is discrete and monotone decreasing. It is sometimes referred to as the log-series distribution or logarithmic distribution. - The distribution was first discussed as a modeling tool for animal populations in a 1943 article by English scientist R. A. Fisher. Since then, the distribution has been used in a number of areas, including botany, survival analysis, and finance. In particular, the log-series distribution has been used to successfully illustrate large-scale phenomena such as population growth, as well as small-scale behavior such as the number of products purchased by an individual in a specified time period. It has also been used in stochastics (in relation to stochastic processes such as the Yule–Furry process, the linear birth-death process, and the Pólya process) and has been generalized to model various events across a wide spectrum of scientific fields.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a log-series distribution. Distributed[x,LogSeriesDistribution[θ]], written more concisely as xLogSeriesDistribution[θ], can be used to assert that a random variable x is distributed according to a log-series distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[LogSeriesDistribution[θ],x] and CDF[LogSeriesDistribution[θ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
- DistributionFitTest can be used to test if a given dataset is consistent with a log-series distribution, EstimatedDistribution to estimate a log-series parametric distribution from given data, and FindDistributionParameters to fit data to a log-series distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic log-series distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic log-series distribution.
- TransformedDistribution can be used to represent a transformed log-series distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a log-series distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving log-series distributions.
- LogSeriesDistribution is related to a number of other statistical distributions. LogSeriesDistribution can be applied in conjunction with Poisson compounding to obtain a NegativeBinomialDistribution in the sense that CompoundPoissonDistribution[μ,LogSeriesDistribution[θ]] is equivalent to NegativeBinomialDistribution[n,p] for suitably defined parameters n and p. LogSeriesDistribution is therefore also related to BinomialDistribution, MultinomialDistribution, and NegativeMultinomialDistribution.
Examples
open all close allScope (7)
Generate a sample of pseudorandom numbers from a logarithmic series distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Applications (2)
Number of items per order form follows log series distribution with ![]() . Find the probability of at least 3 items per order:
. Find the probability of at least 3 items per order:
Find the most likely number of items per order:
Find the average number of items per order:
The number of accident claims per policy per year from an insurance company:
Since most policies have no accidents or one accident reported, the data may be modeled by a logarithmic series distribution:
Find the probability that there are 2 or more accidents reported for a given policy:
Properties & Relations (2)
The probability of getting any real number except a positive integer is zero:
Log-series distribution is a limit of zero-truncated NegativeBinomialDistribution:
Possible Issues (2)
LogSeriesDistribution is not defined when θ is not strictly between zero and one:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
See Also
Tech Notes
Related Guides
History
Text
Wolfram Research (2007), LogSeriesDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/LogSeriesDistribution.html.
CMS
Wolfram Language. 2007. "LogSeriesDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LogSeriesDistribution.html.
APA
Wolfram Language. (2007). LogSeriesDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LogSeriesDistribution.html
BibTeX
@misc{reference.wolfram_2025_logseriesdistribution, author="Wolfram Research", title="{LogSeriesDistribution}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/LogSeriesDistribution.html}", note=[Accessed: 26-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_logseriesdistribution, organization={Wolfram Research}, title={LogSeriesDistribution}, year={2007}, url={https://reference.wolfram.com/language/ref/LogSeriesDistribution.html}, note=[Accessed: 26-February-2026]}