MixtureDistribution

MixtureDistribution[{w1,…,wn},{dist1,…,distn}]

represents a mixture distribution whose CDF is given as a sum of the CDFs of the component distributions disti, each with weight wi.

Details

  • The cumulative distribution function for value 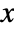is proportional to 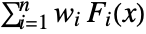, where 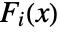is the CDF for disti.
  • The distributions disti need to be all continuous or all discrete, and have the same dimensionality.
  • The weights wi can be any non-negative real numbers.
  • MixtureDistribution can be used with such functions as Mean, CDF, and RandomVariate, etc.

Examples

open allclose all

Basic Examples  (3)

Define a mixture of two continuous distributions:

Define a mixture of two discrete distributions:

Define a multivariate mixture:

Scope  (30)

Basic Uses  (10)

A mixture with numeric weights:

Cumulative distribution function:

A mixture with symbolic weights:

Probability density function:

The weights control the contribution by each distribution:

Two univariate continuous distributions:

The mixture combines the densities according to their weights:

Two bivariate continuous distributions:

The mixture combines the densities according to their weights:

Two univariate discrete distributions:

Probability density function:

Plot a density function for different weights:

Mean and variance:

Two multivariate discrete distributions:

Probability density function:

Generate random numbers:

Several univariate continuous distributions:

Moments:

Factorial moments:

Central moments:

Cumulants:

Several univariate discrete distributions:

Generating functions:

Estimate weights in a mixture:

Parametric Distributions  (5)

Define a mixture of two different continuous distributions:

Probability density function:

Hazard function:

In the limit the exponential distribution component dominates:

Define a mixture of two distributions with different supports:

Probability density function for a few values of the weight:

Define a mixture of two different univariate discrete distributions:

Probability density function:

Cumulative distribution function:

Moments can be obtained numerically:

Define a mixture of two different multivariate discrete distributions:

Probability density function:

Covariance:

Define a mixture distribution of multivariate uniform distributions:

Cumulative distribution function:

Nonparametric Distributions  (3)

Define a mixture with SmoothKernelDistribution:

The mixture combines the densities according to their weights:

Define a mixture with EmpiricalDistribution:

The mixture combines the cumulative distribution functions according to their weights:

Plot the cumulative distribution function:

Define a mixture with HistogramDistribution:

The mixture combines the densities according to their weights:

Derived Distributions  (10)

Define a mixture distribution with components given by MixtureDistribution:

The PDF is piecewise continuous:

The mean is a convex combination of the means of the components:

Find which components cause the mean of the mixture to be indeterminate:

Find a mixture distribution of the OrderDistribution of the minimum and the maximum:

Compare the probability density functions:

The mean of the mixture distribution:

Compare to the average of the means of order distributions:

Find the mixture distribution of a TruncatedDistribution:

The probability density function is not continuous:

The mean can be computed explicitly:

Find the probability density function of the mixture distribution with a ProductDistribution:

Define a mixture distribution with a TransformedDistribution:

Probability density function:

Define a mixture distribution of a MarginalDistribution:

Characteristic function:

Define a mixture with a CensoredDistribution:

Probability density function:

A mixture with a ParameterMixtureDistribution:

PDFs of scaled mixture components and mixture distribution:

Define a mixture distribution with a CopulaDistribution:

Mixture of compatible QuantityDistribution evaluates to QuantityDistribution:

Evaluate the mean:

Plot the PDF:

Automatic Simplifications  (2)

One component mixture simplifies to the input distribution:

A mixture with zero weights will reduce the number of input distributions:

A mixture with one zero weight will return unevaluated:

Applications  (7)

Find the percentage of values between and :

Between and :

Package it up as a function using NProbability:

Determine the maximal variance of a mixture:

The heights of females in the United States follow normal distribution with mean 64 inches and standard deviation of 2 inches, while the heights of males in the United States follow normal distribution with mean 70 inches and standard deviation of 2 inches. If the population ratio of males to females is 1.1, then the heights of the whole population have the following bimodal distribution:

Simulate a typical distribution of heights in a town of population 100:

Find the probability that a person is at least 73 inches tall:

A binary transmission is sent with 0 coded as a voltage signal and 1 as a voltage signal. 1 is sent with probability but the signal is corrupted by white noise. Find the PDF of the received signal:

Simulate transmission at the receiver for p=0.4 and v=1:

To distinguish between the two signals, the voltage difference must be bigger:

MixtureDistribution can be used to create multimodal models:

The magnitudes of earthquakes in the United States in the selected years have two modes:

Find an estimated distribution from possible mixtures of two normal distributions:

Compare the histogram to the PDF of the estimated distribution:

Find the probability of an earthquake of magnitude 7 or higher:

Find the mean earthquake magnitude:

Simulate magnitudes of the next 30 earthquakes:

The average city and highway mileage for midsize cars follows a binormal distribution:

Show the distribution of city and highway mileage:

Assuming 65% of the driving is done in the city, the mileage follows a MixtureDistribution:

Find the average mileage:

Gaussian mixture model is commonly used for the purpose of image segmentation. Image is represented as an array of pixels. A pixel is a scalar (or vector) which shows the intensity (or color):

Visualize the distribution of pixel values via Histogram:

Fit the pixel values to a three-component Gaussian mixture with EstimatedDistribution:

Label each pixel with maximum a posterior probability (MAP) estimate:

Visualize the result:

Properties & Relations  (8)

A mixture with weights w is equivalent to one with weights w/Total[w]:

Compare PDFs:

The PDF of a mixture is a convex combination of the PDF of its components:

The CDF of a mixture is a convex combination of the CDF of its components:

The moments of a mixture are a convex combination of the moments of its components:

A moment of general order:

A ParameterMixtureDistribution with a discrete weight, assuming a finite number of values, can be represented as a mixture distribution:

Compare PDFs:

A ParameterMixtureDistribution with a discrete weight, assuming a countable number of values, can be approximated by a mixture distribution:

Compare approximations for different quantiles as cut-offs:

Approximating a ParameterMixtureDistribution with a continuous weight by a mixture distribution:

Compare PDFs:

A KernelMixtureDistribution is a MixtureDistribution derived from data:

Neat Examples  (3)

A mixture of two binormal distributions:

A variety of distributional shapes from Gaussian mixtures:

A multivariate Gaussian mixture:

Wolfram Research (2010), MixtureDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MixtureDistribution.html (updated 2016).

Text

Wolfram Research (2010), MixtureDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MixtureDistribution.html (updated 2016).

CMS

Wolfram Language. 2010. "MixtureDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MixtureDistribution.html.

APA

Wolfram Language. (2010). MixtureDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MixtureDistribution.html

BibTeX

@misc{reference.wolfram_2024_mixturedistribution, author="Wolfram Research", title="{MixtureDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MixtureDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mixturedistribution, organization={Wolfram Research}, title={MixtureDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MixtureDistribution.html}, note=[Accessed: 21-November-2024 ]}