RandomSample[{e1,e2,…},n]
gives a pseudorandom sample of n of the ei.
RandomSample[{w1,w2,…}{e1,e2,…},n]
gives a pseudorandom sample of n of the ei chosen using weights wi.
RandomSample[{e1,e2,…}]
gives a pseudorandom permutation of the ei.


RandomSample
RandomSample[{e1,e2,…},n]
gives a pseudorandom sample of n of the ei.
RandomSample[{w1,w2,…}{e1,e2,…},n]
gives a pseudorandom sample of n of the ei chosen using weights wi.
RandomSample[{e1,e2,…}]
gives a pseudorandom permutation of the ei.
Details

- RandomSample is also known as simple random sampling or sampling without replacement.
- RandomSample[{e1,e2,…},n] never samples any of the
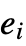 more than once.
more than once. - RandomSample[{e1,e2,…},n] samples each of the
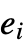 with equal probability.
with equal probability. - RandomSample[{e1,e2,…},UpTo[n]] gives a sample of n of the ei, or as many as are available.
- RandomSample[i;;j;;k,n] may be used to sample the Span from i to j in steps of k.
- RandomSample gives a different sequence of pseudorandom choices whenever you run the Wolfram Language. You can start with a particular seed using SeedRandom.
- A Method option to SeedRandom can be given to specify the pseudorandom generator used.
Examples
open all close allBasic Examples (3)
Scope (4)
Properties & Relations (3)
Use SeedRandom to get repeatable random values:
Use BlockRandom to block one use of RandomSample from affecting others:
RandomSample of size 1 follows the same distribution as RandomChoice:
See Also
RandomChoice RandomInteger SeedRandom BlockRandom Permutations Subsets Span Downsample
Function Repository: BootstrappedEstimate Shuffle
Tech Notes
Related Guides
Text
Wolfram Research (2007), RandomSample, Wolfram Language function, https://reference.wolfram.com/language/ref/RandomSample.html (updated 2015).
CMS
Wolfram Language. 2007. "RandomSample." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/RandomSample.html.
APA
Wolfram Language. (2007). RandomSample. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RandomSample.html
BibTeX
@misc{reference.wolfram_2025_randomsample, author="Wolfram Research", title="{RandomSample}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/RandomSample.html}", note=[Accessed: 22-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_randomsample, organization={Wolfram Research}, title={RandomSample}, year={2015}, url={https://reference.wolfram.com/language/ref/RandomSample.html}, note=[Accessed: 22-January-2026]}