Wolfram Language & System Documentation Center

MarginalDistribution

MarginalDistribution[dist,k]

represents a univariate marginal distribution of the k coordinate from the multivariate distribution dist.

MarginalDistribution[dist,{k₁,k₂,…}]

represents a multivariate marginal distribution of the {k₁,k₂,…} coordinates.

Details

The distribution dist can be either a discrete or continuous multivariate distribution.
For a discrete multivariate distribution dist with PDF 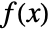, the PDF of MarginalDistribution[dist,{k₁,…,k_m}] is given by 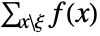where ξ={x_k₁,…,x_{k_m}}.
For a continuous multivariate distribution dist with PDF 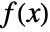, the PDF of MarginalDistribution[dist,{k₁,…,k_m}] is given by 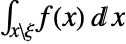where ξ={x_k₁,…,x_{k_m}}.
MarginalDistribution can be used with such functions as Mean, CDF, and RandomVariate, etc.

Examples

open all close all

Basic Examples (3)

One-dimensional marginal distributions:

Two-dimensional marginal distributions:

Marginal distributions can be used like any other distribution:

Scope (34)

Basic Uses (8)

Find the second univariate marginal distribution:

Multivariate marginals depend on the coordinate order given:

Univariate marginals behave as univariate distributions:

Find distribution functions:

Multivariate marginals behave like a multivariate distribution:

Find distribution functions:

Special moments are computed for each univariate marginal distribution:

Compare moments of marginal distributions with the moment of original distribution:

A general multivariate moment cannot typically be found from marginal moments:

Quantile functions can be computed for univariate marginal distributions:

Find the quantile functions:

Or special medians:

Generate random variates from MarginalDistribution:

Compare the histogram to the plot of the PDF of the marginal distribution:

Estimate distribution parameters:

Define a trivariate probability distribution:

Find marginal distributions:

Find the covariance matrix of :

The variances of the marginals form the diagonal of the covariance matrix of :

Parametric Distributions (2)

The marginal distributions of many multivariate parametric distributions automatically simplify:

The univariate marginals follow BetaDistribution:

The multivariate marginals follow DirichletDistribution:

In some cases, marginal distributions will not automatically simplify:

Univariate marginals simplify to a BinomialDistribution:

The multivariate marginals do not simplify:

The resulting marginal can still be used like any other distribution:

Nonparametric Distributions (3)

Find marginals of an EmpiricalDistribution:

Cumulative distribution function of the marginal distributions:

Find marginals for a SmoothKernelDistribution:

Find marginals of a HistogramDistribution:

Compare to the histograms of the components:

Derived Distributions (9)

Find the marginal distribution of a MarginalDistribution:

The second marginal of is the third marginal of :

Find marginals of a CopulaDistribution:

Find marginals of a TruncatedDistribution:

Probability density function:

Find marginals of a MixtureDistribution:

Each marginal distribution is the mixture of marginals:

Compare with the marginal distributions of the components:

Marginals of a MixtureDistribution are mixtures of marginals:

Plot a probability density function for both marginals:

Create a bivariate distribution using marginal distributions:

Compare a PDF of the original distribution with the ProductDistribution of marginals:

Compare covariance matrices:

Find marginal distributions of a TransformedDistribution:

Find marginal distributions of a ParameterMixtureDistribution:

Visualize the probability density function:

Find marginal distributions of an OrderDistribution:

Probability density function:

Mean:

Variance:

Marginals of a QuantityDistribution give QuantityDistribution:

Univariate marginal:

Multivariate marginal:

Automatic Simplifications (12)

Discrete Parametric Distributions (3)

Marginals of multivariate DiscreteUniformDistribution again follow a uniform distribution:

Univariate marginals of MultivariatePoissonDistribution follow PoissonDistribution:

Multivariate marginals again follow multivariate Poisson distribution:

Univariate marginals of MultinomialDistribution follow BinomialDistribution:

Continuous Parametric Distributions (6)

Marginals of BinormalDistribution follow NormalDistribution:

All univariate marginals of MultinormalDistribution follow NormalDistribution:

Multivariate marginals of MultinormalDistribution are multivariate normal:

Marginals of multivariate UniformDistribution follow uniform distribution:

One-dimensional marginals of DirichletDistribution follow BetaDistribution:

Multivariate marginals of DirichletDistribution again follow Dirichlet distribution:

Univariate marginals of MultivariateTDistribution follow StudentTDistribution:

Univariate marginals of LogMultinormalDistribution follow LogNormalDistribution:

Multivariate marginals of LogMultinormalDistribution again follow log-multinormal distribution:

Derived Distributions (3)

Marginals of ProductDistribution are the component distributions:

One-dimensional marginal:

A two-dimensional marginal is also defined by ProductDistribution:

Univariate marginals of a CopulaDistribution are the marginals used in the specification:

Marginal distributions of a MixtureDistribution are the mixtures of component marginals:

Applications (5)

Visualize univariate marginal distributions together with a bivariate distribution:

Plot the univariate marginals:

Show the results together:

The city-highway mileage for a midsize car is given by a binormal distribution. Find the city mileage distribution:

Plot the probability density function:

Find the average city mileage:

The male weight and height follow a binormal distribution. Find the height distribution:

Probability density function:

Find the median height for males:

Find the lower quartile:

Express the height distribution in meters:

A fair coin is flipped three times with the objective of getting three tails. Find the join distribution of the number of failures in the form of getting a head on the second or on the third flip:

Probability density function:

Find the average number of failures of each kind:

Find the total number of failures of both kinds:

Simulate the number of failures by getting a head on the second or on the third flip:

A university campus lies completely within twin cities and . On a day there are on average 10 car accidents on campus and the joint distribution of the number of accidents per day in both cities is: