StudentTDistribution

StudentTDistribution[ν]

represents a standard Student distribution with ν degrees of freedom.

StudentTDistribution[μ,σ,ν]

represents a Student distribution with location parameter μ, scale parameter σ, and ν degrees of freedom.

Details

The probability density for value in a Student distribution with degrees of freedom is proportional to . »
For following a Student distribution with location parameter μ, scale parameter σ and ν degrees of freedom, follows a standard Student distribution with ν degrees of freedom.
For integer ν, the Student distribution gives the distribution of the deviation from the true mean of the observed mean for a sample of ν values from a normal distribution, normalized by standard deviation of the sample.
StudentTDistribution allows μ to be any real number and σ and ν to be any positive real numbers.
StudentTDistribution allows μ and σ to be any quantities of the same unit dimension, and ν to be any dimensionless quantity. »
StudentTDistribution can be used with such functions as Mean, CDF, and RandomVariate. »

Background & Context

StudentTDistribution[μ,σ,ν] represents a continuous statistical distribution defined and supported over the set of real numbers and parametrized by a real number μ (called a "location parameter") and by positive real numbers σ and ν (called a "scale parameter" and the "degrees of freedom", respectively), which together determine the overall behavior of its probability density function (PDF). In general, the PDF of a Student distribution is unimodal with a single "peak" (i.e. a global maximum), though its overall shape (its height, its spread, and the horizontal location of its maximum) is determined by the values of μ, σ, and ν. In addition, the tails of the PDF are "fat", in the sense that the PDF decreases algebraically rather than decreasing exponentially for large values of . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The one-parameter form StudentTDistribution[ν] is equivalent to StudentTDistribution[0,1,ν] and is sometimes referred to as "the" Student 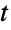distribution, while the three-parameter form StudentTDistribution[μ,σ,ν] is sometimes referred to as the generalized Student distribution.
The Student distribution was first devised by English statistician William Gosset (published under the pseudonym "Student") in 1908. Gosset showed that for integer ν, the Student distribution is precisely the distribution of the deviation of the observed mean from the true population mean given a sample of ν normalized and normally-distributed random variates. The -distribution is widely used throughout statistics and is an often-utilized tool in hypothesis testing, analysis of variance tests, Bayesian analysis, and stochastic processes. The distribution has also found extensive use across a number of different fields to model phenomena including stock price fluctuations, phase derivatives of telecommunications components, noise models, and image analysis.
RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Student distribution. Distributed[x,StudentTDistribution[μ,σ,ν]], written more concisely as xStudentTDistribution[μ,σ,ν], can be used to assert that a random variable x is distributed according to a Student distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
The probability density and cumulative distribution functions for Student distributions may be given using PDF[StudentTDistribution[μ,σ,ν],x] and CDF[StudentTDistribution[μ,σ,ν],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
DistributionFitTest can be used to test if a given dataset is consistent with a Student distribution, EstimatedDistribution to estimate a Student parametric distribution from given data, and FindDistributionParameters to fit data to a Student distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Student distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Student distribution.
TransformedDistribution can be used to represent a transformed Student distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Student distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Student distributions.
StudentTDistribution is related to a number of other distributions. StudentTDistribution is a special case of NoncentralStudentTDistribution, in the sense that the PDF of StudentTDistribution[ν] is precisely the same as that of NoncentralStudentTDistribution[ν,0] and is also generalized by PearsonDistribution in various ways. StudentTDistribution[ν] tends to NormalDistribution[] as ν→∞, while the PDF of StudentTDistribution can be obtained as transformations (TransformedDistribution) of FRatioDistribution, ChiSquareDistribution, and NormalDistribution and as a parameter mixture (ParameterMixtureDistribution) of NormalDistribution with GammaDistribution. StudentTDistribution is also closely related to CauchyDistribution, MultivariateTDistribution, and ChiDistribution.

Examples

open allclose all

Basic Examples (8)

Probability density function:

Cumulative distribution function:

Mean and variance:

Median:

Probability density function of a generalized Student distribution:

Cumulative distribution function of a generalized Student distribution:

Mean and variance of a generalized Student distribution:

Median of a generalized Student distribution:

Scope (8)

Generate a sample of pseudorandom numbers from a Student distribution:

Compare its histogram to the PDF:

Distribution parameters estimation:

Estimate the distribution parameters from sample data:

Compare the density histogram of the sample with the PDF of the estimated distribution:

A Student distribution is symmetric and hence skewness is 0 if defined:

Kurtosis:

Adding scale and location parameters does not change the kurtosis:

In the limit, kurtosis is the same as for NormalDistribution:

Different moments with closed forms as functions of parameters:

Moment:

Closed form for symbolic order:

Moment for generalized Student distribution:

CentralMoment:

Closed form for symbolic order:

CentralMoment for generalized Student distribution:

Closed form for symbolic order:

FactorialMoment:

FactorialMoment for generalized Student distribution:

Cumulant:

Cumulant for generalized Student distribution:

Hazard function:

For generalized Student distribution:

Quantile function:

For generalized Student distribution:

Consistent use of Quantity in parameters yields QuantityDistribution:

Find quartiles:

Applications (2)

Compute ‐values for a ‐test with degrees of freedom and alternative hypothesis :

Alternative hypothesis :

StudentTDistribution is used in exact (small) sampling theory. Define -statistics:

If data comes from a normal distribution, then the -statistics follow a StudentTDistribution, even for data that is a sample of small size (less than 30):