MomentGeneratingFunction[dist,t]
gives the moment-generating function for the distribution dist as a function of the variable t.
MomentGeneratingFunction[dist,{t1,t2,…}]
gives the moment-generating function for the multivariate distribution dist as a function of the variables t1, t2, … .


MomentGeneratingFunction
MomentGeneratingFunction[dist,t]
gives the moment-generating function for the distribution dist as a function of the variable t.
MomentGeneratingFunction[dist,{t1,t2,…}]
gives the moment-generating function for the multivariate distribution dist as a function of the variables t1, t2, … .
Details
- MomentGeneratingFunction is also called a raw moment-generating function.
- MomentGeneratingFunction[dist,t] is equivalent to Expectation[Exp[t x],xdist].
- MomentGeneratingFunction[dist, {t1,t2,…}] is equivalent to Expectation[Exp[t.x],xdist] for vectors t and x.
- The i
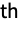 moment can be extracted from a moment-generating function mgf through SeriesCoefficient[mgf,{t,0,i}]i!.
moment can be extracted from a moment-generating function mgf through SeriesCoefficient[mgf,{t,0,i}]i!.
Examples
open all close allBasic Examples (3)
Scope (5)
Applications (3)
Find the moment-generating function of the sum of random variates:
Check that it is equal to the product of generating functions:
When ![]() it coincides with the mgf of BinomialDistribution:
it coincides with the mgf of BinomialDistribution:
Confirm with TransformedDistribution:
Reconstruct the PDF of a positive real random variate from its moment-generating function:
Illustrate the central limit theorem on the example of PoissonDistribution:
Find the moment-generating function for the standardized random variate:
Find the moment-generating function for the sum of ![]() standardized random variates rescaled by
standardized random variates rescaled by ![]() :
:
Compare with the moment-generating function of a standard normal distribution:
Properties & Relations (5)
MomentGeneratingFunction is equivalent to Expectation of ![]() :
:
MomentGeneratingFunction is an exponential generating function for the sequence of moments:
Use SeriesCoefficient to find moment ![]() :
:
Use Moment directly:
MomentGeneratingFunction is a LaplaceTransform for positive random variables:
MomentGeneratingFunction is a ZTransform for discrete positive random variates:
Possible Issues (2)
For some distributions with long tails, moments of only several low orders are defined:
Correspondingly, MomentGeneratingFunction is undefined:
Analytic continuation of CharacteristicFunction can sometimes be defined:
MomentGeneratingFunction is not always known in closed form:
Use Moment to evaluate particular moments:
Neat Examples (1)
History
Text
Wolfram Research (2010), MomentGeneratingFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/MomentGeneratingFunction.html.
CMS
Wolfram Language. 2010. "MomentGeneratingFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MomentGeneratingFunction.html.
APA
Wolfram Language. (2010). MomentGeneratingFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MomentGeneratingFunction.html
BibTeX
@misc{reference.wolfram_2025_momentgeneratingfunction, author="Wolfram Research", title="{MomentGeneratingFunction}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/MomentGeneratingFunction.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_momentgeneratingfunction, organization={Wolfram Research}, title={MomentGeneratingFunction}, year={2010}, url={https://reference.wolfram.com/language/ref/MomentGeneratingFunction.html}, note=[Accessed: 09-March-2026]}