CharacteristicFunction[dist,t]
gives the characteristic function for the distribution dist as a function of the variable t.
CharacteristicFunction[dist,{t1,t2,…}]
gives the characteristic function for the multivariate distribution dist as a function of the variables t1, t2, ….


CharacteristicFunction
CharacteristicFunction[dist,t]
gives the characteristic function for the distribution dist as a function of the variable t.
CharacteristicFunction[dist,{t1,t2,…}]
gives the characteristic function for the multivariate distribution dist as a function of the variables t1, t2, ….
Details
- CharacteristicFunction[dist,t] is equivalent to Expectation[Exp[ t x],xdist].
- CharacteristicFunction[dist,{t1,t2,…}] is equivalent to Expectation[Exp[ t.x],xdist] for vectors t and x.
- The k
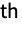 moment can be extracted from a characteristic function cf through SeriesCoefficient[cf,{t,0,k}]k! (-)k.
moment can be extracted from a characteristic function cf through SeriesCoefficient[cf,{t,0,k}]k! (-)k.
Examples
open all close allBasic Examples (4)
Scope (8)
Characteristic function for a specific continuous distribution:
Characteristic function for a specific discrete distribution:
Characteristic function at a particular value:
Characteristic function evaluated numerically:
Obtain a result at any precision:
Compute the characteristic function for a formula distribution:
Find the characteristic function for a parameter mixture distribution:
Characteristic function for the slice distribution of a random process:
Applications (7)
Compute the raw moments for a Poisson distribution:
First 5 raw moments using derivatives of the characteristic function at the origin:
Use Moment directly:
Compute mixed raw moments for a multivariate ![]() distribution:
distribution:
Use Moment to obtain raw moments directly:
Find raw moments of a Student ![]() distribution from its characteristic function:
distribution from its characteristic function:
Compute ![]() to extract moments by taking limits from the right:
to extract moments by taking limits from the right:
Evaluate the limits from the left:
Only the first four moments are defined, as confirmed by using Moment directly:
Use inverse Fourier transform to compute the PDF corresponding to a characteristic function:
Illustrate the central limit theorem on the example of symmetric LaplaceDistribution:
Find the characteristic function of the rescaled random variate:
Compute the large ![]() limit of the cf of the sum of
limit of the cf of the sum of ![]() such i.i.d. random variates:
such i.i.d. random variates:
Compare with the characteristic function of a standard normal variate:
Use smooth characteristic function to construct the upper bound for the distribution density of ErlangDistribution:
Plot the upper bounds and the original density:
Verify that the sum ![]() where
where ![]() are independent identically distributed BernoulliDistribution[1/2] variates tends in distribution to UniformDistribution[] for large
are independent identically distributed BernoulliDistribution[1/2] variates tends in distribution to UniformDistribution[] for large ![]() :
:
Use a combinatorial equality for product ![]() :
:
Take the limit and compare it to the characteristic function of the UniformDistribution:
Properties & Relations (5)
CharacteristicFunction is the Expectation of ![]() for real
for real ![]() :
:
The characteristic function is related to all other generating functions when they exist:
The cf of a continuous distribution is equivalent to FourierTransform of its PDF:
The cf of a discrete distribution is equivalent to FourierSequenceTransform of its PDF:
The PDF is the inverse Fourier transform of the cf for continuous distributions:
The PDF is the inverse Fourier sequence transform of the cf for discrete distributions:
Neat Examples (1)
Visualize real and imaginary parts of CharacteristicFunction for random instances of BinomialDistribution:
Tech Notes
Text
Wolfram Research (2007), CharacteristicFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/CharacteristicFunction.html (updated 2010).
CMS
Wolfram Language. 2007. "CharacteristicFunction." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2010. https://reference.wolfram.com/language/ref/CharacteristicFunction.html.
APA
Wolfram Language. (2007). CharacteristicFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CharacteristicFunction.html
BibTeX
@misc{reference.wolfram_2025_characteristicfunction, author="Wolfram Research", title="{CharacteristicFunction}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/CharacteristicFunction.html}", note=[Accessed: 22-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_characteristicfunction, organization={Wolfram Research}, title={CharacteristicFunction}, year={2010}, url={https://reference.wolfram.com/language/ref/CharacteristicFunction.html}, note=[Accessed: 22-February-2026]}