FourierSequenceTransform[expr,n,ω]
gives the Fourier sequence transform of expr.
FourierSequenceTransform[expr,{n1,n2,…},{ω1,ω2,…}]
gives the multidimensional Fourier sequence transform.


FourierSequenceTransform
FourierSequenceTransform[expr,n,ω]
gives the Fourier sequence transform of expr.
FourierSequenceTransform[expr,{n1,n2,…},{ω1,ω2,…}]
gives the multidimensional Fourier sequence transform.
Details and Options

- FourierSequenceTransform is also known as discrete-time Fourier transform (DTFT).
- FourierSequenceTransform[expr,n,ω] takes a sequence whose n
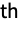 term is given by expr, and yields a function of the continuous parameter ω.
term is given by expr, and yields a function of the continuous parameter ω. - The Fourier sequence transform of
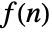 is by default defined to be
is by default defined to be 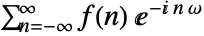 .
. - The Fourier sequence transform of
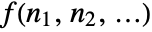 is by default periodic with a period of
is by default periodic with a period of 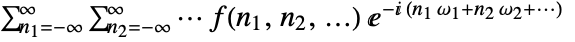 .
. - The multidimensional transform of
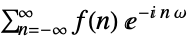 is defined to be
is defined to be 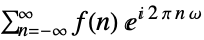 .
. - The following options can be given:
-
Assumptions $Assumptions assumptions on parameters FourierParameters {1,1} parameters to define the discrete-time Fourier transform GenerateConditions False whether to generate results that involve conditions on parameters - Common settings for FourierParameters include:
-
{1,1} 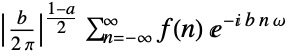
default settings {1,2Pi} 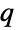
period 1 {a,b} 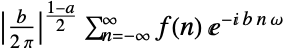
general setting
Examples
open all close allBasic Examples (2)
Scope (4)
Options (2)
FourierParameters (1)
Use a non-default setting for FourierParameters:
Properties & Relations (5)
FourierSequenceTransform is defined by a doubly infinite sum:
FourierSequenceTransform and InverseFourierSequenceTransform are inverses:
FourierSequenceTransform is closely related to ZTransform:
A discrete analog of FourierTransform being closely related to LaplaceTransform:
FourierSequenceTransform provides a ![]() -analog generating function:
-analog generating function:
FourierSequenceTransform is closely related to BilateralZTransform:
See Also
InverseFourierSequenceTransform Fourier FourierTransform FourierCoefficient ZTransform BilateralZTransform DiscreteConvolve Sum
Function Repository: NFourierSequenceTransform
Related Guides
History
Text
Wolfram Research (2008), FourierSequenceTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierSequenceTransform.html.
CMS
Wolfram Language. 2008. "FourierSequenceTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FourierSequenceTransform.html.
APA
Wolfram Language. (2008). FourierSequenceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierSequenceTransform.html
BibTeX
@misc{reference.wolfram_2025_fouriersequencetransform, author="Wolfram Research", title="{FourierSequenceTransform}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/FourierSequenceTransform.html}", note=[Accessed: 23-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_fouriersequencetransform, organization={Wolfram Research}, title={FourierSequenceTransform}, year={2008}, url={https://reference.wolfram.com/language/ref/FourierSequenceTransform.html}, note=[Accessed: 23-January-2026]}