Pi

Pi

is , with numerical value .

Details

Background & Context

  • Pi is the symbol representing the mathematical constant 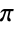, which can also be input as ∖[Pi]. Pi is defined as the ratio of the circumference of a circle to its diameter and has numerical value 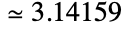. Pi arises in many mathematical computations including trigonometric expressions, special function values, sums, products, and integrals as well as in formulas from a wide range of mathematical and scientific fields.
  • When Pi is used as a symbol, it is propagated as an exact quantity. While many expressions involving Pi (e.g. Cos[Pi/10]) are automatically expanded in terms of simpler functions, expansion and simplification of more complicated expressions involving Pi (e.g. Cos[Pi/15]) may require use of functions such as FunctionExpand and FullSimplify.
  • Pi is known to be both irrational and transcendental, meaning it can be expressed neither as a ratio of integers nor as the root of any integer polynomial. While it is not known if Pi is normal (meaning the digits in its base- 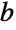expansion are equally distributed) to any base, its known digits are very uniformly distributed.
  • Pi can be evaluated to arbitrary numerical precision by means of the Chudnovsky formula using N. In fact, calculating the first million decimal digits of Pi takes only a fraction of a second on a modern desktop computer. RealDigits can be used to return a list of digits of Pi and ContinuedFraction to obtain terms of its continued fraction expansion.
  • Most angle-related functions in the Wolfram Language take radian measures as their arguments and return radian measures as results. The symbol Degree, which is equal to Pi/180, can therefore be used as a multiplier when entering values in degree measures (e.g. Cos[30 Degree]).

Examples

open allclose all

Basic Examples  (3)

Pi can be entered as p:

Evaluate to any precision:

Do an exact numerical computation:

Scope  (1)

Find the millionth digit of in base 10:

Applications  (5)

Find an area of a circle:

The first 20 digits of in base 10:

Trigonometric functions have arguments in radians:

Many mathematical functions and operations give results involving π:

Properties & Relations  (2)

Various symbolic relations are automatically used:

Pi is treated as a constant in differentiation:

Neat Examples  (2)

Walk corresponding to the binary digits of :

Terms in the continued fraction:

Wolfram Research (1988), Pi, Wolfram Language function, https://reference.wolfram.com/language/ref/Pi.html (updated 1996).

Text

Wolfram Research (1988), Pi, Wolfram Language function, https://reference.wolfram.com/language/ref/Pi.html (updated 1996).

CMS

Wolfram Language. 1988. "Pi." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Pi.html.

APA

Wolfram Language. (1988). Pi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Pi.html

BibTeX

@misc{reference.wolfram_2024_pi, author="Wolfram Research", title="{Pi}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Pi.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_pi, organization={Wolfram Research}, title={Pi}, year={1996}, url={https://reference.wolfram.com/language/ref/Pi.html}, note=[Accessed: 21-November-2024 ]}