CentralMomentGeneratingFunction[dist,t]
gives the central moment-generating function for the distribution dist as a function of the variable t.
CentralMomentGeneratingFunction[dist,{t1,t2,…}]
gives the central moment-generating function for the multivariate distribution dist as a function of the variables t1, t2, ….


CentralMomentGeneratingFunction
CentralMomentGeneratingFunction[dist,t]
gives the central moment-generating function for the distribution dist as a function of the variable t.
CentralMomentGeneratingFunction[dist,{t1,t2,…}]
gives the central moment-generating function for the multivariate distribution dist as a function of the variables t1, t2, ….
Details
- CentralMomentGeneratingFunction[dist,t] is given by Expectation[Exp[t(x-μ)],xdist] where μ=Mean[dist].
- CentralMomentGeneratingFunction[dist, {t1,t2,…}] is equivalent to Expectation[Exp[t.(x-μ)],xdist] for vectors t and x and where μ=Mean[dist].
- The i
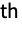 central moment can be extracted from a central moment-generating function cmgf through SeriesCoefficient[cmgf,{t,0,i}]i!.
central moment can be extracted from a central moment-generating function cmgf through SeriesCoefficient[cmgf,{t,0,i}]i!.
Examples
open all close allBasic Examples (3)
Scope (5)
Applications (3)
Find the cmgf of the sum of random variates:
Alternatively, compute the product of cmgfs of summands:
When ![]() it coincides with the central moment-generating function of ErlangDistribution:
it coincides with the central moment-generating function of ErlangDistribution:
Confirm with TransformedDistribution:
Find the first few central moments of the sum of ![]() i.i.d. non-central
i.i.d. non-central ![]() random variates:
random variates:
Illustrate the central limit theorem using ExponentialDistribution:
Find the cmgf of the exponential variate rescaled to have variance ![]() :
:
Find the large ![]() limit of the cmgf of the sum of
limit of the cmgf of the sum of ![]() such variates:
such variates:
Properties & Relations (3)
The cmgf is the moment-generating function times ![]() :
:
Use SeriesCoefficient to find central moment ![]() :
:
Compare with CentralMoment:
CentralMomentGeneratingFunction is an exponential generating function for the sequence of central moments:
Possible Issues (2)
For some distributions with long tails, central moments of only several low orders are defined:
Correspondingly, CentralMomentGeneratingFunction is undefined:
CentralMomentGeneratingFunction is not always known in closed form:
Use CentralMoment to evaluate particular central moments:
Related Guides
History
Text
Wolfram Research (2010), CentralMomentGeneratingFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html.
CMS
Wolfram Language. 2010. "CentralMomentGeneratingFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html.
APA
Wolfram Language. (2010). CentralMomentGeneratingFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html
BibTeX
@misc{reference.wolfram_2025_centralmomentgeneratingfunction, author="Wolfram Research", title="{CentralMomentGeneratingFunction}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html}", note=[Accessed: 04-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_centralmomentgeneratingfunction, organization={Wolfram Research}, title={CentralMomentGeneratingFunction}, year={2010}, url={https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html}, note=[Accessed: 04-January-2026]}