GaussianMatrix

GaussianMatrix[r]

gives a matrix that corresponds to a Gaussian kernel of radius r.

GaussianMatrix[{r,σ}]

gives a matrix corresponding to a Gaussian kernel with radius r and standard deviation σ.

GaussianMatrix[r,{n1,n2}]

gives a matrix formed from the n1^(th) derivative of the Gaussian with respect to rows and the n2^(th) derivative with respect to columns.

GaussianMatrix[r,{{n11,n12},{n21,n22},…}]

gives a matrix formed from the sums of the ni1 and ni2 derivatives.

GaussianMatrix[{{r1,r2,…},σ},…]

gives an array corresponding to a Gaussian kernel with radius ri in the i^(th) index direction.

Details and Options

  • GaussianMatrix[r] gives values that approximate 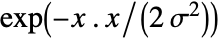at index position 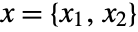from the center, where σ=r/2.
  • By default, the elements of GaussianMatrix[r] sum to 1.
  • GaussianMatrix[…,{n1,n2}] by default constructs discrete derivatives as finite differences.
  • GaussianMatrix[r,{{2,0},{0,2}}] gives a matrix formed from the Laplacian of a Gaussian.
  • GaussianMatrix[{Automatic,σ,f},…] constructs a matrix just large enough to include at least a fraction f of the discrete integral of a Gaussian in each direction.
  • Any of the r, σ, and f can be lists, specifying different values for different directions.
  • For integer r, GaussianMatrix[r,…] yields a 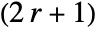× 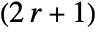matrix.
  • For noninteger r, the value of r is effectively rounded to an integer.
  • The following options can be specified:
  • Method "Bessel"how to determine matrix elements
    Standardized Truewhether to rescale and shift the matrix to account for truncation
    WorkingPrecision Automaticthe precision with which to compute matrix elements
  • Possible settings for the Method option are "Bessel" and "Gaussian".
  • With the default option setting Method->"Bessel", GaussianMatrix[r] has elements proportional to product_(i=1)^2exp(-sigma^2) TemplateBox[{{x, _, i}, {sigma, ^, 2}}, BesselI], yielding a kernel with optimal discrete convolution properties.
  • For Method->"Bessel", derivatives of the Gaussian are obtained by the finite difference operator. GaussianMatrix[{r,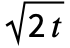}] satisfies the finite difference equation .
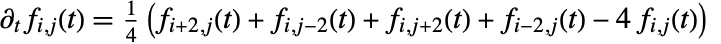  • With Method->"Gaussian", GaussianMatrix[r] has elements proportional to the raw continuous functional form .
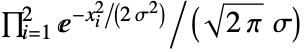  • For Method->"Gaussian", derivatives of the Gaussian are proportional to the partial derivatives of the functional form. The GaussianMatrix[{r,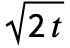}] approximately satisfies the differential equation .
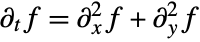  • With Standardized->True, the proportionality factor ensures that the elements of GaussianMatrix[r] sum to 1. However, the elements of GaussianMatrix[r,{n1,n2,…}] with at least one nonzero ni will sum to 0, and the sum of the elements, weighted in each direction by 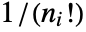times the distance from the origin to the power of ni, will be 1.
  • With Standardized->False, no proportionality factor is used.

Background & Context

  • GaussianMatrix is a constructor function that returns a matrix having a Gaussian profile. Such matrices are typically used as kernels in image convolution for smoothing or taking derivatives of images.
  • The function ImageConvolve can be used to perform convolution on an image using a Gaussian matrix kernel. Other functions that create smoothing or derivative kernel matrices include ShenCastanMatrix and SavitzkyGolayMatrix. Note that non-smooth kernels can also be used to smooth images. Binary kernels commonly used for this purpose include DiskMatrix, DiamondMatrix, and other similar functions.

Examples

open allclose all

Basic Examples  (3)

Compute and plot a Gaussian matrix:

Compute and plot a Gaussian vector:

First derivative of a Gaussian matrix in the horizontal dimension:

Scope  (6)

Gaussian matrix of radius 20:

3D plot of the matrix:

Gaussian matrix with varying standard deviations:

First derivative of a Gaussian matrix in the vertical dimension:

First derivative of a Gaussian matrix in the horizontal dimension:

3D visualization of the matrix:

Create and visualize a 3D Gaussian array:

A 3D derivative kernel:

A 3D derivative kernel along the first dimension:

Generalizations & Extensions  (4)

Generate an exact symbolic Gaussian matrix:

Use a radius of twice the standard deviation:

Use a radius sufficient to at least fill the desired fraction of the Gaussian:

Using a smaller radius would not have provided the desired fraction:

Use a standard deviation such that a specified radius provides a desired fraction of the Gaussian:

Options  (10)

Method  (4)

With Method->"Bessel", the derivative is computed using a finite difference:

With Method->"Gaussian", the continuous derivative is used:

A Gaussian matrix appropriate for discrete convolution:

A Gaussian matrix sampled from the continuum:

Standardized  (5)

A normalized Gaussian vector:

A normalized Gaussian matrix:

An unnormalized Gaussian vector:

The total of the unnormalized matrix approaches 1 as the ratio of its size to its standard deviation increases:

A shifted Gaussian derivative:

A shifted Gaussian derivative is also rescaled:

A Gaussian derivative that is not standardized:

Shifts and rescalings are performed using a discrete normalization for all methods:

WorkingPrecision  (1)

A machine-precision Gaussian vector:

An exact symbolic Gaussian vector:

A high-precision Gaussian vector:

Applications  (3)

Smooth a signal:

Apply Gaussian blur to an image:

Compute vertical derivative of an image:

Possible Issues  (1)

At least one of the radius or standard deviation must be specified in each direction:

Wolfram Research (2008), GaussianMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/GaussianMatrix.html (updated 2015).

Text

Wolfram Research (2008), GaussianMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/GaussianMatrix.html (updated 2015).

CMS

Wolfram Language. 2008. "GaussianMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GaussianMatrix.html.

APA

Wolfram Language. (2008). GaussianMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaussianMatrix.html

BibTeX

@misc{reference.wolfram_2024_gaussianmatrix, author="Wolfram Research", title="{GaussianMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GaussianMatrix.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gaussianmatrix, organization={Wolfram Research}, title={GaussianMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/GaussianMatrix.html}, note=[Accessed: 21-November-2024 ]}