DiamondMatrix

DiamondMatrix[r]

gives a matrix whose elements are 1 in a diamond-shaped region that extends r index positions to each side, and are 0 otherwise.

DiamondMatrix[r,w]

gives a w×w matrix containing a diamond-shaped region of 1s.

DiamondMatrix[{r1,r2,…},…]

yields an array whose elements are 1 in a diamond-shaped region that extends ri index positions in the i^(th) direction.

Details

  • The diamond of 1s is always at the center of the region.
  • In DiamondMatrix[r] or DiamondMatrix[{r1,…}] the matrix or array is sized so as to just include all nonzero elements.
  • The region of 1s is taken to be the best discrete approximation to a diamond-shaped region possible given the size of the matrix.
  • DiamondMatrix[All,w] gives a w×w matrix containing a diamond shape that is as large as possible.
  • DiamondMatrix[…,{w1,w2,…}] gives a w1×w2×… array.
  • DiamondMatrix[{r1,…,rn},w] gives a w×…×w array.
  • DiamondMatrix[All,{w1,…,wn}] gives a w1×…×wn array containing a diamond-shaped region that is as large as possible.
  • The parameter r need not be an integer; in general elements are 1 if their Manhattan distance from the center is not more than .
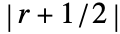  • For integer r, DiamondMatrix[r] yields a 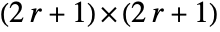matrix.

Examples

open allclose all

Basic Examples  (1)

This computes and plots a square diamond-shaped matrix of radius 10:

Scope  (5)

Create a rectangular diamond-shaped matrix:

Put a diamond inside a bigger matrix:

Extend the diamond to the boundaries of the matrix:

Automatically choose an odd width to just fit the diamond:

Extend the diamond to the given width, and automatically choose the height:

Wolfram Research (2008), DiamondMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/DiamondMatrix.html.

Text

Wolfram Research (2008), DiamondMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/DiamondMatrix.html.

CMS

Wolfram Language. 2008. "DiamondMatrix." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiamondMatrix.html.

APA

Wolfram Language. (2008). DiamondMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiamondMatrix.html

BibTeX

@misc{reference.wolfram_2024_diamondmatrix, author="Wolfram Research", title="{DiamondMatrix}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/DiamondMatrix.html}", note=[Accessed: 15-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_diamondmatrix, organization={Wolfram Research}, title={DiamondMatrix}, year={2008}, url={https://reference.wolfram.com/language/ref/DiamondMatrix.html}, note=[Accessed: 15-November-2024 ]}