SavitzkyGolayMatrix

✖
`SavitzkyGolayMatrix`

✖

SavitzkyGolayMatrix[r,k]

gives a matrix corresponding to a smoothing kernel of radius r for performing polynomial regression of degree k.

✖

SavitzkyGolayMatrix[{r₁,r₂},{k₁,k₂}]

gives a matrix for performing polynomial regression of degree k₁ over a window of radius r₁ along rows, and degree k₂ over a window of radius r₂ along columns.

✖

SavitzkyGolayMatrix[r,k,n]

gives a matrix for performing the n derivative of a polynomial regression of degree k.

✖

SavitzkyGolayMatrix[{r₁,r₂… },{k₁,k₂,…},…]

gives an array using the specified parameters for each direction i.

Details and Options

SavitzkyGolayMatrix[r,k] can be used to smooth data using a local polynomial regression.
SavitzkyGolayMatrix[r,k,n] can be used to compute the derivatives of data using a local polynomial regression.
The elements of SavitzkyGolayMatrix[r,k] sum to 1.
SavitzkyGolayMatrix allows any of r, k, and n to be lists, specifying different values for different directions.
For integer r, SavitzkyGolayMatrix[r,…] yields a 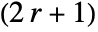× 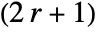matrix.
For noninteger r, the value of r is effectively rounded to an integer.
SavitzkyGolayMatrix accepts a WorkingPrecision option. The default setting is WorkingPrecision->MachinePrecision.
SavitzkyGolayMatrix can be used in functions such as ListConvolve and ImageConvolve.

Examples

open allclose all

Basic Examples (3)Summary of the most common use cases

Compute a matrix kernel for quadratic interpolation over a window of radius 5:

In[1]:=1

✖

https://wolfram.com/xid/0rbwyufk3vwcp620zh07m-0ncnyn

Out[1]=1

Compute a smoothing kernel of length 11 using a cubic interpolation:

In[1]:=1

✖

https://wolfram.com/xid/0rbwyufk3vwcp620zh07m-22u2gu

Out[1]=1

Plot the vector:

In[2]:=2

✖

https://wolfram.com/xid/0rbwyufk3vwcp620zh07m-q6s93b

Out[2]=2

A Savitzky–Golay matrix to compute first derivatives in the horizontal dimension:

In[1]:=1

✖

https://wolfram.com/xid/0rbwyufk3vwcp620zh07m-hr9xln

Out[1]=1

Scope (3)Survey of the scope of standard use cases

Create a 3D smoothing kernel:

In[1]:=1

✖

https://wolfram.com/xid/0rbwyufk3vwcp620zh07m-7tjw52

Out[1]=1

A 3D derivative kernel:

In[1]:=1

✖

https://wolfram.com/xid/0rbwyufk3vwcp620zh07m-69h4z8

Out[1]=1

A 3D derivative kernel along the first dimension:

In[1]:=1

✖

https://wolfram.com/xid/0rbwyufk3vwcp620zh07m-ilcb8h

Out[1]=1

Options (1)Common values & functionality for each option

WorkingPrecision (1)

By default, machine precision is used in internal computations:

In[1]:=1

✖

https://wolfram.com/xid/0rbwyufk3vwcp620zh07m-6s1p9r

Out[1]=1

Use exact precision:

In[2]:=2

✖

https://wolfram.com/xid/0rbwyufk3vwcp620zh07m-0jvtv

Out[2]=2

Applications (2)Sample problems that can be solved with this function

Use a 2D SavitzkyGolayMatrix as a smoothing kernel in ImageConvolve:

In[1]:=1

✖

https://wolfram.com/xid/0rbwyufk3vwcp620zh07m-6rinpk

Out[1]=1

Compute the horizontal derivative of an image:

In[1]:=1

✖

https://wolfram.com/xid/0rbwyufk3vwcp620zh07m-65ej4n

Out[1]=1

Properties & Relations (1)Properties of the function, and connections to other functions

The order of the polynomial does not extend beyond twice the window size:

In[1]:=1

✖

https://wolfram.com/xid/0rbwyufk3vwcp620zh07m-u9xgm

Out[1]=1

Top