represents a Maxwell distribution with scale parameter σ.


MaxwellDistribution
represents a Maxwell distribution with scale parameter σ.
Details
- MaxwellDistribution is also known as Maxwell–Boltzmann distribution.
- The probability density for value
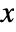 in a Maxwell distribution is proportional to
in a Maxwell distribution is proportional to 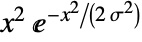 for
for 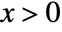 , and is zero for
, and is zero for 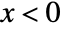 . »
. » - MaxwellDistribution allows σ to be any positive real number.
- MaxwellDistribution allows σ to be a quantity of any unit dimension. »
- MaxwellDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- MaxwellDistribution[σ] represents a continuous statistical distribution supported over the interval
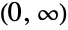 and parametrized by a positive real number σ (called a "scale parameter") that determines the overall behavior of its probability density function (PDF). In general, the PDF of a Maxwell distribution is unimodal with a single "peak" (i.e. a global maximum), though its overall shape (height, spread, and horizontal location of its maximum) is determined by the values of σ. In addition, the PDF of the Maxwell distribution has tails that are "thin" in the sense that its PDF decreases exponentially rather than algebraically for large values of
and parametrized by a positive real number σ (called a "scale parameter") that determines the overall behavior of its probability density function (PDF). In general, the PDF of a Maxwell distribution is unimodal with a single "peak" (i.e. a global maximum), though its overall shape (height, spread, and horizontal location of its maximum) is determined by the values of σ. In addition, the PDF of the Maxwell distribution has tails that are "thin" in the sense that its PDF decreases exponentially rather than algebraically for large values of 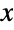 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Maxwell distribution is also sometimes referred to as the Maxwell-Boltzmann distribution and as the Maxwell speed distribution.
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Maxwell distribution is also sometimes referred to as the Maxwell-Boltzmann distribution and as the Maxwell speed distribution. - The Maxwell distribution was first described in the 1860s by Scottish physicist James Clark Maxwell. It became an indispensable model in statistical mechanics following later investigations by Austrian physicist Ludwig Boltzmann. The Maxwell distribution describes the speeds of particles in ideal gases under the assumption that the particles have reached thermodynamic equilibrium and have minimal interaction with one another. As such, the distribution is considered the foundation of the kinetic theory of gases and is a tool in the related field of Maxwell-Boltzmann statistics that attempts to describe the distribution of non-interacting particles on a more general level. The distribution has also been used to describe phenomena in various fields including chemistry, reliability and risk analysis, signal processing, and Bayesian analysis.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Maxwell distribution. Distributed[x,MaxwellDistribution[σ]], written more concisely as xMaxwellDistribution[σ], can be used to assert that a random variable x is distributed according to a Maxwell distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for Maxwell distributions may be given using PDF[MaxwellDistribution[σ],x] and CDF[MaxwellDistribution[σ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Maxwell distribution, EstimatedDistribution to estimate a Maxwell parametric distribution from given data, and FindDistributionParameters to fit data to a Maxwell distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Maxwell distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Maxwell distribution.
- TransformedDistribution can be used to represent a transformed Maxwell distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Maxwell distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Maxwell distributions.
- MaxwellDistribution is related to a number of other distributions. It is a special case of ChiDistribution (the PDF of MaxwellDistribution[1] is precisely the same as that of ChiDistribution[3]), ChiSquareDistribution (CDF[MaxwellDistribution[1],Sqrt[x]] is identically CDF[ChiSquareDistribution[3],x]), and GammaDistribution (the PDF of MaxwellDistribution[σ] and GammaDistribution[3/2,Sqrt[2] σ,2,0] are the same). The exponential decay behavior of MaxwellDistribution makes it qualitatively similar to NormalDistribution, RayleighDistribution, BetaDistribution, and ExponentialDistribution. By way of its relationship to ChiDistribution and ChiSquareDistribution, MaxwellDistribution is also related to NakagamiDistribution, NoncentralChiSquareDistribution, and HalfNormalDistribution.
Examples
open all close allBasic Examples (4)
Scope (7)
Generate a sample of random numbers from a Maxwell distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness and kurtosis are constant:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (2)
Consider vectors with standard normal components:
The ![]() angle in spherical coordinates follows a uniform distribution:
angle in spherical coordinates follows a uniform distribution:
The norm will follow a Maxwell distribution:
Velocity density function along any direction of a gas molecule follows a normal distribution with mean 0 and standard deviation ![]() . The standard deviation for molecular hydrogen at 573 K is:
. The standard deviation for molecular hydrogen at 573 K is:
The distribution of the speeds of molecules in a hydrogen gas at 573 K is given:
Find the probability that a hydrogen molecule has speed at least 4000 meters per second:
Find the average speed of such a molecule:
Compare the ratios of the average speed and the RMS speed to the most probable speed:
Simulate the speed of 100 hydrogen molecules in the above conditions:
Properties & Relations (7)
Maxwell distribution is closed under scaling by a positive factor:
The variance is proportional to the square of the mean:
Relationships to other distributions:
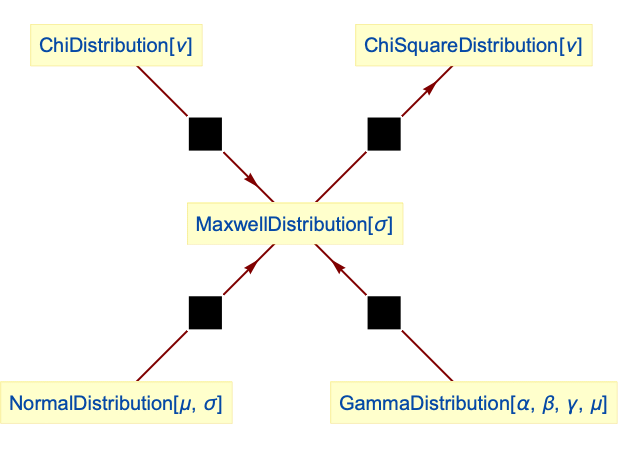
MaxwellDistribution with ![]() is a special case of ChiDistribution:
is a special case of ChiDistribution:
Square of MaxwellDistribution with ![]() is a special case of ChiSquareDistribution:
is a special case of ChiSquareDistribution:
MaxwellDistribution is a special case of GammaDistribution:
The norm of three standard normally distributed variables follows Maxwell distribution:
Possible Issues (2)
MaxwellDistribution is not defined when σ is not a positive real number:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
See Also
Tech Notes
Related Guides
Text
Wolfram Research (2007), MaxwellDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MaxwellDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "MaxwellDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MaxwellDistribution.html.
APA
Wolfram Language. (2007). MaxwellDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MaxwellDistribution.html
BibTeX
@misc{reference.wolfram_2025_maxwelldistribution, author="Wolfram Research", title="{MaxwellDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MaxwellDistribution.html}", note=[Accessed: 06-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_maxwelldistribution, organization={Wolfram Research}, title={MaxwellDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MaxwellDistribution.html}, note=[Accessed: 06-March-2026]}