TrimmedVariance
TrimmedVariance[list,f]
gives the variance of the elements in list after dropping a fraction f of the smallest and largest elements.
TrimmedVariance[list,{f1,f2}]
gives the variance when a fraction f1 of the smallest elements and a fraction f2 of the largest elements are removed.
TrimmedVariance[list]
gives the 5% trimmed variance TrimmedVariance[list,0.05].
TrimmedVariance[dist,…]
gives the trimmed variance of a univariate distribution dist.
Details
- TrimmedVariance gives a robust estimate of the variance by excluding extreme values.
- The trimming fraction is determined by the parameters f1 and f2, which indicate the fraction f1 of the smallest elements and the fraction f2 of the largest elements to be removed.
- TrimmedVariance[list,{f1,f2}] gives the variance of Sort[list,Less]〚1+
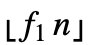;;n-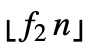
〛 where n equals the length of list. - TrimmedVariance[{{x1,y1,…},{x2,y2,…},…},f] gives {TrimmedVariance[{x1,x2,…},f],TrimmedVariance[{y1,y2,…},f],…}.
- TrimmedVariance[dist,{f1,f2}] gives Variance[TruncatedDistribution[Quantile[dist,{f1,1-f2}],dist]] for a univariate distribution dist.
Examples
open allclose allBasic Examples (4)
Scope (10)
Data (9)
Exact input yields exact output:
Approximate input yields approximate output:
TrimmedVariance for a matrix gives columnwise variances:
Trimmed variance works with large arrays:
SparseArray data can be used just like dense arrays:
Trimmed variance of a TimeSeries:
Trimmed variance depends only on the values:
Trimmed variance works with data involving quantities:
Compute trimmed variance of dates:
Applications (2)
Obtain a robust estimate of dispersion when outliers are present:
Extreme values have a large influence on the Variance:
Find a trimmed variance for the heights of children in a class:
Plot the trimmed variance as a function of trimmed fraction:
Plot the square root of the trimmed variance with respect to the trimmed mean:
Properties & Relations (5)
A 0% TrimmedVariance is equivalent to Variance:
TrimmedVariance approaches 0 as f approaches 1/2:
TrimmedVariance of a distribution is the variance of its TruncatedDistribution:
Variance of the TruncatedDistribution with appropriate bounds:
TrimmedVariance of a sample gives an estimate of the variance of a truncated distribution:
Variance of the TruncatedDistribution with appropriate bounds:
TrimmedVariance drops the data beyond a certain quantile level, then computes the sample variance:
WinsorizedVariance clips the data beyond a certain quantile level, then computes the sample variance:
Plot the sorted data against the sample with elements removed and the clipped sample:
Possible Issues (1)
TrimmedVariance requires numeric values:
Text
Wolfram Research (2017), TrimmedVariance, Wolfram Language function, https://reference.wolfram.com/language/ref/TrimmedVariance.html (updated 2024).
CMS
Wolfram Language. 2017. "TrimmedVariance." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/TrimmedVariance.html.
APA
Wolfram Language. (2017). TrimmedVariance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TrimmedVariance.html