SpatialMedian[{x1,x2,…}]
gives the spatial median of the elements ![]() .
.
SpatialMedian[data]
gives the spatial median for several different forms of data.


SpatialMedian
SpatialMedian[{x1,x2,…}]
gives the spatial median of the elements ![]() .
.
SpatialMedian[data]
gives the spatial median for several different forms of data.
Details and Options


- SpatialMedian is also known as geometric median, median center and 1-median.
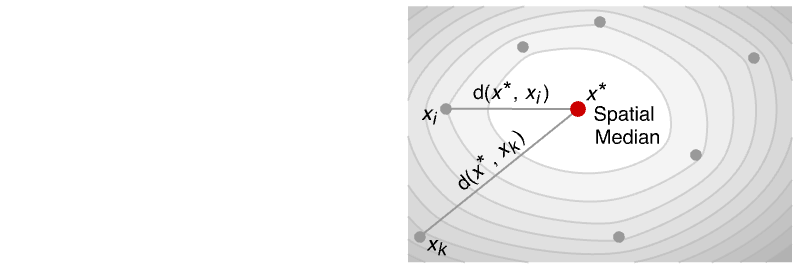
- SpatialMedian is a robust location measure. It gives a point with minimum total distance to every point in the data.
- SpatialMedian is equivalent to
![x^*=ArgMin[sum_(i=1)^nd(x,x_i),x] x^*=ArgMin[sum_(i=1)^nd(x,x_i),x]](Files/SpatialMedian.en/2.png) for the unweighted case and
for the unweighted case and ![x^*=ArgMin[sum_(i=1)^nw_i d(x,x_i),x] x^*=ArgMin[sum_(i=1)^nw_i d(x,x_i),x]](Files/SpatialMedian.en/3.png) for the weighted case.
for the weighted case. - The data data has the following forms and interpretations:
-
{x1,x2,…} univariate numerical data {{x1,y1,…},{x2,y2,…},…} multivariate numerical data {GeoPosition[…],GeoPosition[…],…} list of geodetic positions GeoPosition[…] array of geodetic positions WeightedData[…] data with weights - Under Euclidean distance, SpatialMedian coincides with median in the one-dimensional case. In the multidimensional case, spatial median is unique whenever the points are not collinear.
- The following options can be given:
-
AccuracyGoal Automatic the accuracy sought DistanceFunction Automatic the distance metric to use MaxIterations Automatic maximum number of iterations to use Method Automatic method to use PrecisionGoal Automatic the precision sought WorkingPrecision Automatic the precision used in internal computations - By default, the following distance functions are used for different types of elements:
-
EuclideanDistance numeric data GeoDistance geospatial data - The setting Method{"InitialPoint"{x0,y0,…}} allows for a custom initial point for computing SpatialMedian.
Examples
open all close allBasic Examples (3)
Scope (5)
Same inputs with different precisions:
Spatial median works with WeightedData:
Spatial median of a large array:
Options (4)
DistanceFunction (2)
By default, EuclideanDistance is used for numerical data:
The ChessboardDistance only takes into account the dimension with the largest separation:
DistanceFunction can be given as a symbol:
Method (2)
Specify the initial point for the iterative procedure of spatial median:
"NMinimize" and the method options of FindMinimum can be used:
Use with specified DistanceFunction:
Applications (8)
Obtain a robust estimate of a multivariate location when outliers are present:
Extreme values have a large influence on the Mean:
Consider data from a Gaussian mixture distribution:
Estimate the center with Mean:
The sample mean estimator has a large spread for non-Gaussian data. The standard deviation of the estimator is:
Estimate the center with SpatialMedian:
Assess the spread via bootstrapping. The spatial median has a smaller spread compared to the mean:
Consider the stock prices of five companies: GOOG, MSFT, FB, AAPL and INTC in 2015 as five-dimensional data:
Compute the log returns and estimate the center using Mean and SpatialMedian:
Fit the data with MultivariateTDistribution and extract the location parameters:
Spatial median estimator gives a closer estimate to the location parameters of multivariate t distribution than the empirical mean with the given stock data:
With the number of points equal to 3, spatial median is also the Fermat point:
Create equilateral triangles on each side:
Construct the Fermat point geometrically and compare it with the result of SpatialMedian (red):
Sample points from a convex polygon:
Estimate the center of the polygon by computing the spatial median of random points:
Find the spatial median of California based on the locations of cities:
Find the spatial median of California based on the locations of cities, weighted by population:
Draw the city locations (gray), unweighted spatial median (red) and weighted spatial median (black):
For geo locations that are far enough apart on the surface of the Earth, the spatial median depends significantly on the choice of the distance function:
The spatial median under GeoPosition:
The spatial median of the projected coordinates under EuclideanDistance:
Show the locations of the spatial medians and the cities:
Centroids of geographic entities can be approximated by the spatial median of the uniformly sampled geo locations. Obtain the country polygon of Spain:
Sample points from the region and compute the corresponding spatial median:
Properties & Relations (5)
SpatialMedian is a multivariate location measure:
Mean is also a location measure:
Visualize the data points with spatial median and mean:
SpatialMedian is the L1 location estimator of spatial points:
Compute SpatialMedian from the definition with FindMinimum:
Visualize the sum of distances function:
Mean (or spatial mean) is the L2 location estimator of spatial points:
Compute Mean from the definition with FindMinimum:
Visualize the sum of distances function:
SpatialMedian is the same as Median for univariate data:
SpatialMedian under ManhattanDistance for multivariate data is the same as Median:
SpatialMedian finds a point in the domain that minimizes the sum of distances:
CentralFeature finds a point that belongs to the data that minimizes the sum of distances:
The sum of distances with respect to CentralFeature is greater than or equal to the one with respect to SpatialMedian:
History
Text
Wolfram Research (2017), SpatialMedian, Wolfram Language function, https://reference.wolfram.com/language/ref/SpatialMedian.html.
CMS
Wolfram Language. 2017. "SpatialMedian." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SpatialMedian.html.
APA
Wolfram Language. (2017). SpatialMedian. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SpatialMedian.html
BibTeX
@misc{reference.wolfram_2025_spatialmedian, author="Wolfram Research", title="{SpatialMedian}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/SpatialMedian.html}", note=[Accessed: 23-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_spatialmedian, organization={Wolfram Research}, title={SpatialMedian}, year={2017}, url={https://reference.wolfram.com/language/ref/SpatialMedian.html}, note=[Accessed: 23-January-2026]}