Asymptotic

Asymptotic[expr,xx0]

gives an asymptotic approximation for expr near x0.

Asymptotic[expr,{x,x0,n}]

gives an asymptotic approximation for expr near x0 to order n.

Details and Options

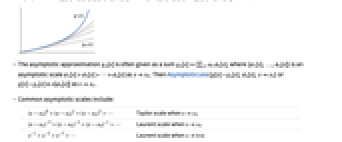
  • Asymptotic is typically used to solve problems for which no exact solution can be found or to get simpler answers for computation, comparison and interpretation. In such cases, an asymptotic approximation often gives enough information for simplifying or solving application problems.
  • Asymptotic[expr,x->x0] computes the leading term in an asymptotic expansion for expr. Use SeriesTermGoal to specify more terms.
  • The expression expr can be any function 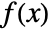, an integral specified by Integrate, LaplaceTransform or InverseLaplaceTransform, a differential equation specified by DSolveValue, etc.
  • The expansion point x0 can be any finite or infinite real or complex number.
  • The approximation order n can be any positive integer or Infinity. If n is set to Infinity and expr is an analytic function of x, then Asymptotic returns the complete power series expansion of expr around x0. »
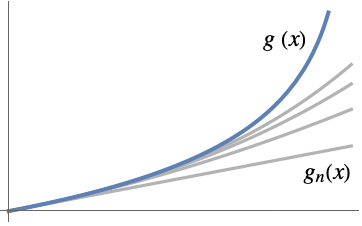
  • If the exact result is g[x] and the asymptotic approximation of order n at x0 is gn[x], then AsymptoticLess[g[x]-gn[x],gn[x]-gn-1[x],xx0] or g[x]-gn[x]∈o[gn[x]-gn-1[x]] as xx0.
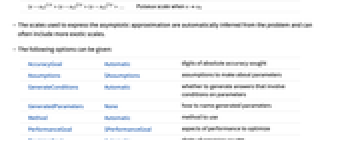
  • The asymptotic approximation gn[x] is often given as a sum gn[x]αkϕk[x], where {ϕ1[x],…,ϕn[x]} is an asymptotic scale ϕ1[x]≻ϕ2[x]≻⋯>ϕn[x] as xx0. Then AsymptoticLess[g[x]-gn[x],ϕn[x],xx0] or g[x]-gn[x]∈o[ϕn[x]] as xx0.
  • Common asymptotic scales include:
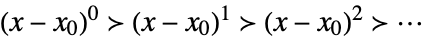
  • Taylor scale when xx0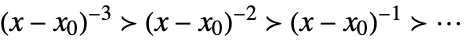
    Laurent scale when xx0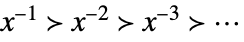
    Laurent scale when x±∞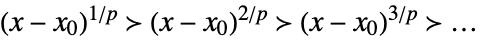
    Puiseux scale when xx0
  • The scales used to express the asymptotic approximation are automatically inferred from the problem and can often include more exotic scales.
  • The following options can be given:
  • AccuracyGoalAutomaticdigits of absolute accuracy sought
    Assumptions$Assumptionsassumptions to make about parameters
    GenerateConditionsAutomaticwhether to generate answers that involve conditions on parameters
    GeneratedParametersNonehow to name generated parameters
    MethodAutomaticmethod to use
    PerformanceGoal$PerformanceGoalaspects of performance to optimize
    PrecisionGoalAutomaticdigits of precision sought
    SeriesTermGoal Automaticnumber of terms in the approximation
    WorkingPrecisionAutomaticthe precision used in internal computations
  • With the default setting of Automatic for GenerateConditions, conditions on parameters are typically not returned in the results from Asymptotic. Answers that include conditions on parameters may be obtained by setting GenerateConditions to True.
  • Possible settings for PerformanceGoal include $PerformanceGoal, "Quality" and "Speed". With the "Quality" setting, Asymptotic typically solves more problems or produces simpler results, but it potentially uses more time and memory.
  • With the default setting of Automatic for WorkingPrecision, AccuracyGoal and PrecisionGoal, Asymptotic may return an asymptotic approximation with a lower precision even if the input has infinite precision.

Examples

open allclose all

Basic Examples  (4)

Find the leading asymptotic approximation for Sin at 0:

Plot the function and the approximation:

Use SeriesTermGoal to obtain a better approximation:

Compute the leading term for an indefinite integral:

Obtain the same result using AsymptoticIntegrate:

Compute the leading term for an inverse Laplace transform:

Compute an asymptotic expansion for a differential equation:

Obtain the same result using AsymptoticDSolveValue:

Scope  (36)

Elementary Functions  (8)

Leading asymptotic term for a polynomial near Infinity:

Plot the function and the approximation:

Rational functions:

Exponential functions:

Polynomial exponential functions:

Rational exponential functions:

Hyperbolic functions:

Logarithmic functions:

Q-functions:

Special Functions  (8)

Leading asymptotic term for Gamma:

Plot the function and the approximation:

Leading asymptotic term for a composite function involving Gamma:

Airy functions:

Plot the function and the approximation:

Bessel functions:

Hypergeometric functions:

Elliptic functions:

Functions involving HarmonicNumber:

Functions involving PolyGamma:

Asymptotic series for QPolyGamma:

Plots of the first three approximations around :

Power Series Representations  (3)

Compute the power series expansion of around 0:

Compute the power series expansion along with the radius of convergence:

Compute the power series expansion of around 0:

Obtain the first seven nonzero terms in the series:

Obtain the same result directly using Asymptotic:

Compute the power series expansion of around 1:

Integrals  (2)

Compute the leading term for an indefinite integral:

Obtain the same result using AsymptoticIntegrate:

Compute the leading term for an Inactive definite integral:

This gives the result for the integral from 0 to Infinity:

Integral Transforms  (13)

Compute the leading term for a Laplace transform:

Compare with a numerical approximation:

Compute the leading term for an inverse Laplace transform:

Compute the leading term for a Mellin transform:

Compute the leading term for an inverse Mellin transform:

Compute the leading term for a Fourier transform:

Compute the leading term for an inverse Fourier transform:

Compute the leading term for a Fourier sine transform:

Compute the leading term for an inverse Fourier sine transform:

Compute the leading term for a Fourier cosine transform:

Compute the leading term for an inverse Fourier cosine transform:

Compute the leading term for a Hankel transform:

Compute the leading term for an inverse Hankel transform:

Compute the leading term for a convolution:

Differential Equations  (2)

Compute the leading term for the asymptotic solution of a linear differential equation:

Obtain the same result using AsymptoticDSolveValue:

Compute the leading term for the asymptotic solution of a DifferentialRoot:

Options  (1)

SeriesTermGoal  (1)

By default, Asymptotic returns the leading term in the asymptotic expansion for a function:

Use SeriesTermGoal to obtain more terms from the expansion:

Applications  (6)

Compute the leading behavior of a function near a point:

Plot the function and the leading behavior:

Compare the leading behavior of a function at 0 and Infinity:

Plot the function and the leading behaviors:

Obtain an asymptotic expansion for a definite integral:

Compare with a numerical approximation:

Find the leading behavior of the solution for a differential equation for large values of :

Find the leading behavior:

Plot the solution along with the leading term:

Find the leading term of the expansion for a meromorphic function at :

Find the leading term at the origin:

The prime number theorem states that is an asymptotic approximation to the prime-counting function TemplateBox[{x}, PrimePi]:

Compare the prime-counting function and the two approximations:

Properties & Relations  (6)

Asymptotic returns a result that is asymptotically equivalent to the input:

Use AsymptoticEquivalent to verify the result:

The result from Asymptotic is equal to the limit at the point if it exists:

Asymptotic typically gives the leading term in the series expansion:

Asymptotic computes approximations for functions of a continuous variable:

DiscreteAsymptotic computes approximations for functions of a discrete variable:

Use AsymptoticExpectation to find an asymptotic approximation of an expectation:

Obtain the asymptotic approximation using Asymptotic:

Use AsymptoticProbability to find an asymptotic approximation of a probability:

Obtain the asymptotic approximation using Asymptotic:

Wolfram Research (2020), Asymptotic, Wolfram Language function, https://reference.wolfram.com/language/ref/Asymptotic.html (updated 2022).

Text

Wolfram Research (2020), Asymptotic, Wolfram Language function, https://reference.wolfram.com/language/ref/Asymptotic.html (updated 2022).

CMS

Wolfram Language. 2020. "Asymptotic." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Asymptotic.html.

APA

Wolfram Language. (2020). Asymptotic. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Asymptotic.html

BibTeX

@misc{reference.wolfram_2025_asymptotic, author="Wolfram Research", title="{Asymptotic}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/Asymptotic.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_asymptotic, organization={Wolfram Research}, title={Asymptotic}, year={2022}, url={https://reference.wolfram.com/language/ref/Asymptotic.html}, note=[Accessed: 21-February-2025 ]}