MellinTransform

MellinTransform[expr,x,s]

gives the Mellin transform of expr.

MellinTransform[expr,{x₁,x₂,…},{s₁,s₂,…}]

gives the multidimensional Mellin transform of expr.

Details and Options

The Mellin transform of a function 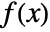is defined to be .
The multidimensional Mellin transform of a function 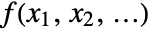is given by .
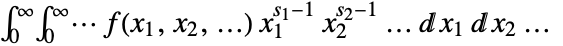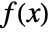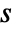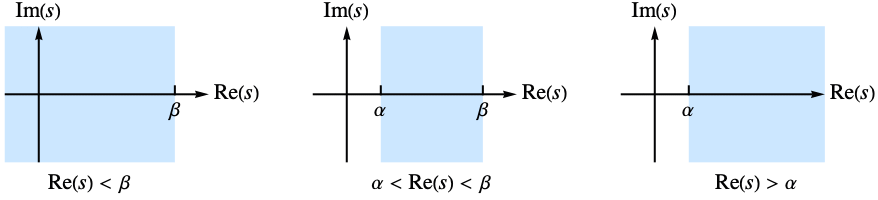
The Mellin transform of exists only for complex values of such that 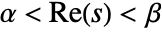. In some cases, this strip of definition may extend to a half-plane.

The following options can be given:

Assumptions	$Assumptions	assumptions on parameters
GenerateConditions	False	whether to generate results that involve conditions on parameters
Method	Automatic	what method to use

In TraditionalForm, MellinTransform is output using .

Examples

open allclose all

Basic Examples (2)

Compute the Mellin transform of a function:

Compute a multivariate Mellin transform:

Scope (16)

Basic Uses (3)

Compute the Mellin transform of a function for a symbolic parameter s:

Use an exact value for the parameter:

Use an inexact value for the parameter:

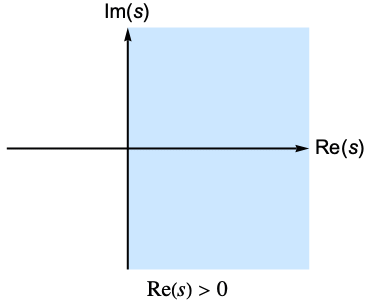
Obtain the condition for validity of a Mellin transform:

The result is valid in the half-plane :

TraditionalForm formatting:

Elementary Functions (3)

Exponential function:

Gaussian function:

General exponential functions:

Composition of logarithmic and exponential functions:

Rational functions:

Mellin transforms of polynomials are given in terms of DiracDelta:

Special Functions (3)

MellinTransform of BesselJ:

BesselK:

Product of Bessel functions:

Exponential integral function ExpIntegralE:

ExpIntegralEi:

MellinTransform of the error function Erf:

Complementary error function Erfc:

Piecewise Functions (3)

MellinTransform of UnitStep:

UnitBox:

UnitTriangle:

Products of functions with UnitStep:

MellinTransform of a Piecewise function:

Generalized Functions (2)

MellinTransform of functions involving HeavisideTheta:

DiracDelta:

Multivariate Functions (2)

Multivariate rational function:

Multivariate exponential function:

Options (5)

Assumptions (1)

Compute the Mellin transform of a function depending on a parameter a:

Obtain a simpler result by specifying assumptions on the parameter:

GenerateConditions (1)

Obtain conditions for validity of the result given by MellinTransform:

GenerateConditions is set to False by default in this case:

Method (3)

Compute a Mellin transform using the default method:

This example is done using table lookup:

Attempting to evaluate this example by a conversion to MeijerG fails:

Evaluate the example using the definition of MellinTransform in terms of Integrate:

The default method uses a conversion to MeijerG for this example:

This is faster than using the definition of MellinTransform in terms of Integrate:

Here, the symbolic method fails because the input is purely numerical:

This example is evaluated using a numerical method based on NIntegrate:

Applications (3)

Use MellinTransform to evaluate $int_0^infty(TemplateBox[{0, t}, BesselJ] TemplateBox[{1, {x, /, t}}, BesselJ])/tdt$ , which may be regarded as a Mellin convolution of the following functions:

Apply MellinTransform to each function:

Obtain the required integral by performing an inverse Mellin transform:

Compute the integral directly using Integrate:

Obtain the same result using MellinConvolve:

Find the general solution of the Bessel equation using MellinTransform:

Apply MellinTransform to the equation:

Use RSolveValue to solve the recurrence equation:

Use InverseMellinTransform to find the required general solution:

Verify the result using DSolveValue:

Use MellinTransform to find the first two terms in the asymptotic expansion for a function that is defined by an infinite series:

Compute the Mellin transform of :

Compute the residues at and to obtain the required asymptotic expansion:

Properties & Relations (11)

Use Asymptotic to compute an asymptotic approximation:

MellinTransform computes the integral :

Obtain the same result using Integrate:

MellinTransform and InverseMellinTransform are mutual inverses:

Verify the relationship for a specific function:

MellinTransform is a linear operator:

The Mellin transform of is given by $(-1)^n TemplateBox[{s, n}, Pochhammer] TemplateBox[{{f, (, x, )}, x, s}, MellinTransform1]$ :

The Mellin transform of is given by $TemplateBox[{{f, (, {a, , x}, )}, x, s}, MellinTransform1]=(TemplateBox[{{f, (, x, )}, x, s}, MellinTransform1])/(a^s)$ for positive values of a:

The Mellin transform of is given by $TemplateBox[{{f, (, {x, ^, a}, )}, x, s}, MellinTransform1]=(TemplateBox[{{f, (, x, )}, x, {s, /, a}}, MellinTransform1])/(TemplateBox[{a}, Abs])$ for real values of a:

The Mellin transform of is given by $TemplateBox[{{{int, _, 0, ^, x}, {{f, (, t, )}, {d, t}}}, x, s}, MellinTransform1]=-(TemplateBox[{{f, (, x, )}, x, {s, +, 1}}, MellinTransform1])/s$ :

The Mellin transform of is given by $TemplateBox[{{{int, _, x, ^, infty}, {{f, (, t, )}, {d, t}}}, x, s}, MellinTransform1]=(TemplateBox[{{f, (, x, )}, x, {s, +, 1}}, MellinTransform1])/s$ :

The Mellin transform of a Mellin convolution is the product of the individual Mellin transforms:

Verify the relationship for a specific pair of functions:

MellinTransform is related to FourierTransform by $sqrt(2 pi) (F_x[f(ⅇ^x)](s))=TemplateBox[{{f, (, x, )}, x, {ⅈ, , s}}, MellinTransform1]$ :

Possible Issues (1)

Different expressions may have the same MellinTransform:

The transforms in these examples have different regions of convergence:

With region of convergence given, the inverse transform gives back the input:

Neat Examples (1)

Create a table of basic Mellin transforms:

Top