FoxH[{{{a1,α1},…,{an,αn}},{{an+1,αn+1},…,{ap,αp}}},{{{b1,β1},…,{bm,βm}},{{bm+1,βm+1},…,{bq,βq}}},z]
is the Fox H-function 
.
FoxH
FoxH[{{{a1,α1},…,{an,αn}},{{an+1,αn+1},…,{ap,αp}}},{{{b1,β1},…,{bm,βm}},{{bm+1,βm+1},…,{bq,βq}}},z]
is the Fox H-function 
.
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
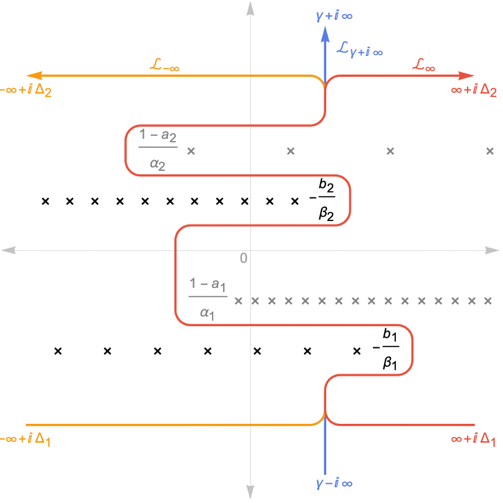
- FoxH generalizes the MeijerG function and is defined by the Mellin–Barnes integral
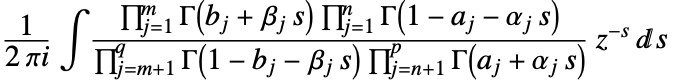where 
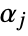and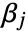 
are positive real numbers and the integration is along a path 
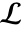separating the poles of 
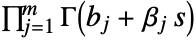from the poles of 
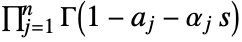. - Three choices are possible for the path
:
a.
is a loop beginning at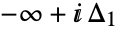 
and ending at 
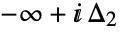and encircling all the poles of 
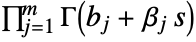once in the positive direction.
b.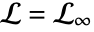
is a loop beginning at 
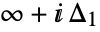and ending at 
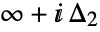and encircling all the poles of 
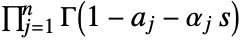once in the negative direction.
c.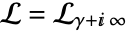
is a contour starting at the point 
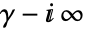and going to 
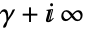such that all the poles of 
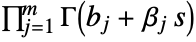are separated from the poles of 
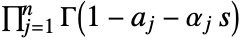. - FoxH specializes to MeijerG if
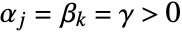for 
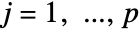and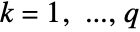 
: 
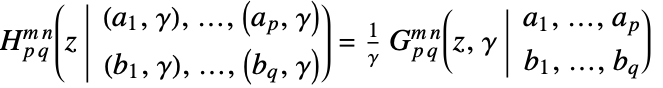. - In many special cases, FoxH is automatically converted to other functions.
- FoxH can be evaluated for arbitrary complex parameters.
- FoxH can be evaluated to arbitrary numerical precision.
- FoxH automatically threads over lists. »
Examples
open all close allBasic Examples (6)
Scope (28)
Numerical Evaluation (7)
The precision of the output tracks the precision of the input:
FoxH takes complex number parameters 
and 
:
FoxH takes complex number arguments:
Evaluate FoxH efficiently at high precision:
Compute the elementwise values of an array using automatic threading:
Or compute the matrix FoxH function using MatrixFunction:
Compute average-case statistical intervals using Around:
Specific Values (3)
Visualization (4)
Plot a family of FoxH functions:
ComplexContourPlot of FoxH[{{{},{}},{{{-1,1/2}},{}}, z]:
Use AbsArgPlot and ReImPlot to plot complex values of FoxH over the real numbers:
Plot FoxH as a function of parameters 
and 
:
Function Properties (5)
Differentiation (2)
First derivative with respect to z:
Higher-order derivative with respect to z:
Formula for the 
derivative of a specific FoxH with respect to z:
Integration (3)
Compute the indefinite integral using Integrate:
Series Expansions (4)
Get the series expansion of some FoxH function at the origin:
The first three approximations of this FoxH function around 
:
Find the series expansion of a general FoxH function at the origin:
Find the series expansion of a general FoxH function at Infinity:
Get the general term in the series expansion using SeriesCoefficient:
Applications (3)
Use FoxHReduce to get the representation of almost any mathematical function in terms of FoxH:
A root of the trinomial equation 
can be written in terms of FoxH:
The roots of the general trinomial 
can also be expressed in terms of FoxH:
Express the PDF of StableDistribution in terms of FoxH for the case of 
:
Evaluate it and compare with the built-in PDF generated using StableDistribution:
Properties & Relations (2)
Use FunctionExpand to expand FoxH into simpler functions:
FoxHReduce returns FoxH representations of functions:
Possible Issues (3)
Neat Examples (1)
Many elementary and special functions are special cases of FoxH:
Text
Wolfram Research (2021), FoxH, Wolfram Language function, https://reference.wolfram.com/language/ref/FoxH.html (updated 2021).
CMS
Wolfram Language. 2021. "FoxH." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/FoxH.html.
APA
Wolfram Language. (2021). FoxH. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FoxH.html