MellinConvolve

MellinConvolve[f,g,x,y]

gives the Mellin convolution with respect to x of the expressions f and g.

MellinConvolve[f,g,{x1,x2,…},{y1,y2,…}]

gives the multidimensional Mellin convolution.

Details and Options

  • The Mellin convolution 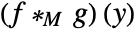of two functions 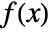and 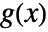is given by .
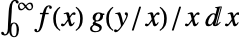  • The multidimensional Mellin convolution of two functions 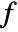and 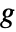is given by .
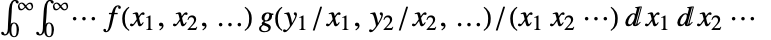  • The following options can be given:
  • Assumptions $Assumptionsassumptions to make about parameters
    GenerateConditions Falsewhether to generate conditions on parameters
    MethodAutomaticmethod to use

Examples

open allclose all

Basic Examples  (2)

Convolve two functions:

Perform a multivariate convolution:

Scope  (8)

Basic Uses  (3)

Compute a Mellin convolution for a symbolic parameter y:

Use an exact value for the parameter:

Use an inexact value for the parameter:

Obtain the condition of validity for a Mellin convolution:

Specify assumptions on a parameter:

Specify a different assumption:

Univariate Convolution  (3)

Elementary functions:

Special functions:

Piecewise functions:

Multivariate Convolution  (2)

Elementary functions:

Piecewise functions:

Options  (2)

Assumptions  (1)

Specify assumptions on a parameter:

GenerateConditions  (1)

Generate conditions for the validity of a Mellin convolution:

Applications  (2)

Compute the PDF for the product of two random variables:

MellinConvolve gives the PDF for the product of these random variables:

Compare with the result from TransformedDistribution:

The integral depends on the parameter α. Find the value of α that lies between 0 and 5 and maximizes the integral. The given integral can be regarded as a Mellin convolution of two functions:

Compute the Mellin convolution of f[x] and g[x]:

Compare with the result given by Integrate:

Plot the integral as a function of α:

Compute the argument that maximizes the integral in 0≤α≤5 using FindArgMax:

Properties & Relations  (8)

MellinConvolve computes the integral :

Scaling:

Commutativity:

Distributivity:

Convolution with DiracDelta:

Derivatives of DiracDelta:

The Mellin transform of a convolution is the product of the individual Mellin transforms:

Derivative of MellinConvolve with respect to y:

Relation between MellinConvolve, MellinTransform, and InverseMellinTransform:

Wolfram Research (2016), MellinConvolve, Wolfram Language function, https://reference.wolfram.com/language/ref/MellinConvolve.html.

Text

Wolfram Research (2016), MellinConvolve, Wolfram Language function, https://reference.wolfram.com/language/ref/MellinConvolve.html.

CMS

Wolfram Language. 2016. "MellinConvolve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MellinConvolve.html.

APA

Wolfram Language. (2016). MellinConvolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MellinConvolve.html

BibTeX

@misc{reference.wolfram_2024_mellinconvolve, author="Wolfram Research", title="{MellinConvolve}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MellinConvolve.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mellinconvolve, organization={Wolfram Research}, title={MellinConvolve}, year={2016}, url={https://reference.wolfram.com/language/ref/MellinConvolve.html}, note=[Accessed: 21-December-2024 ]}