MellinConvolve[f,g,x,y]
给出表达式 f 和 g 关于 x 的 Mellin 卷积 .
MellinConvolve[f,g,{x1,x2,…},{y1,y2,…}]
给出多维度 Mellin 卷积.


MellinConvolve
MellinConvolve[f,g,x,y]
给出表达式 f 和 g 关于 x 的 Mellin 卷积 .
MellinConvolve[f,g,{x1,x2,…},{y1,y2,…}]
给出多维度 Mellin 卷积.
更多信息和选项
- 两个函数
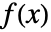 和
和 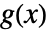 的 Mellin 卷积
的 Mellin 卷积 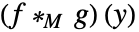 为
为 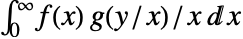 .
. - 两个函数
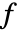 和
和 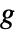 的多维度 Mellin 卷积为
的多维度 Mellin 卷积为 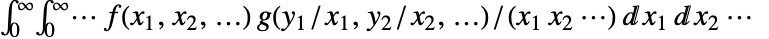 .
. - 可以给出下列选项:
-
Assumptions $Assumptions 参数的设定 GenerateConditions False 是否给出参数的条件 Method Automatic 使用的方法
范例
打开所有单元 关闭所有单元范围 (8)
应用 (2)
计算两个随机变量的积的 PDF:
MellinConvolve 给出这些随机变量的积的 PDF:
与 TransformedDistribution 的结果相比较:
积分 ![]() 取决于参数 α. 求 α 位于 0 和 5 之间的值并最大化积分. 该积分可被视为两个函数的 Mellin 卷积:
取决于参数 α. 求 α 位于 0 和 5 之间的值并最大化积分. 该积分可被视为两个函数的 Mellin 卷积:
与 Integrate 的结果相比较:
用 FindArgMax 计算使得在 0≤α≤5 的积分最大化的参数:
属性和关系 (8)
MellinConvolve 计算积分 ![]() :
:
与 DiracDelta 卷积:
DiracDelta 的导数:
MellinConvolve 关于 y 的导数:
MellinConvolve、MellinTransform 和 InverseMellinTransform 之间的关系:
相关指南
-
▪
- 积分变换
文本
Wolfram Research (2016),MellinConvolve,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MellinConvolve.html.
CMS
Wolfram 语言. 2016. "MellinConvolve." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MellinConvolve.html.
APA
Wolfram 语言. (2016). MellinConvolve. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MellinConvolve.html 年
BibTeX
@misc{reference.wolfram_2025_mellinconvolve, author="Wolfram Research", title="{MellinConvolve}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MellinConvolve.html}", note=[Accessed: 05-October-2025]}
BibLaTeX
@online{reference.wolfram_2025_mellinconvolve, organization={Wolfram Research}, title={MellinConvolve}, year={2016}, url={https://reference.wolfram.com/language/ref/MellinConvolve.html}, note=[Accessed: 05-October-2025]}