Convolve

Convolve[f,g,x,y]

gives the convolution with respect to x of the expressions f and g.

Convolve[f,g,{x1,x2,…},{y1,y2,…}]

gives the multidimensional convolution.

Details and Options

  • Convolve is also known as Fourier convolution, acausal convolution or bilateral convolution.
  • The convolution 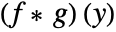of two functions 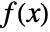and 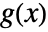is given by .
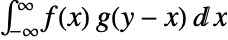  • The multidimensional convolution is given by .
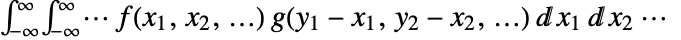  • The following options can be given:
  • Assumptions $Assumptionsassumptions to make about parameters
    GenerateConditions Falsewhether to generate conditions on parameters
    MethodAutomaticmethod to use
    PrincipalValueFalsewhether to use principal value integrals

Examples

open allclose all

Basic Examples  (3)

Convolve a function with DiracDelta:

Convolve two unit pulses:

Convolve two exponential functions and plot the result:

Scope  (5)

Univariate Convolution  (3)

The convolution gives the product integral of translates:

Elementary functions:

A convolution typically smooths the function:

For this family, they all have unit area:

Multivariate Convolution  (2)

The convolution gives the product integral of translates:

Convolution with multivariate delta functions acts as a point operator:

Convolution with a function of bounded support acts as a filter:

Generalizations & Extensions  (1)

Multiplication by UnitStep effectively gives the convolution on a finite interval:

Options  (2)

Assumptions  (1)

Specify assumptions on a variable or parameter:

GenerateConditions  (1)

Generate conditions for the range of a parameter:

Applications  (5)

Obtain a particular solution for a linear ordinary differential equation using convolution:

Obtain the step response of a linear, time-invariant system given its impulse response h:

The step response of the system:

Convolving the PDF of UniformDistribution with itself gives a TriangularDistribution:

UniformSumDistribution[n] is the convolution of n UniformDistribution[] PDFs:

ErlangDistribution[k,λ] is the convolution of k ExponentialDistribution[λ] PDFs:

Properties & Relations  (7)

Convolve computes an integral over the real line:

Convolution with DiracDelta gives the function itself:

Scaling:

Commutativity:

Distributivity:

The Laplace transform of a causal convolution is a product of the individual transforms:

The Fourier transform of a convolution is related to the product of the individual transforms:

Interactive Examples  (1)

This demonstrates the convolution operation :

Wolfram Research (2008), Convolve, Wolfram Language function, https://reference.wolfram.com/language/ref/Convolve.html.

Text

Wolfram Research (2008), Convolve, Wolfram Language function, https://reference.wolfram.com/language/ref/Convolve.html.

CMS

Wolfram Language. 2008. "Convolve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Convolve.html.

APA

Wolfram Language. (2008). Convolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Convolve.html

BibTeX

@misc{reference.wolfram_2024_convolve, author="Wolfram Research", title="{Convolve}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Convolve.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_convolve, organization={Wolfram Research}, title={Convolve}, year={2008}, url={https://reference.wolfram.com/language/ref/Convolve.html}, note=[Accessed: 21-December-2024 ]}