Convolve
更多信息和选项

- Convolve 又称傅立叶卷积 (Fourier convolution)、非因果卷积 (acausal convolution) 或双边卷积 (bilateral convolution).
- 两个函数
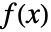 和
和 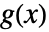 的卷积
的卷积 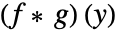 是
是 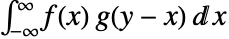 .
. - 多维卷积是
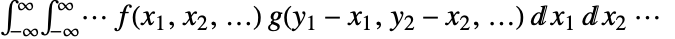 .
. - 可以给出下列选项:
-
Assumptions $Assumptions 关于参数的假设 GenerateConditions False 是否生成参数的条件 Method Automatic 使用的方法 PrincipalValue False 是否使用主值积分
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (5)
推广和延伸 (1)
UnitStep 的乘法实际上给出有限区间上的卷积:
应用 (5)
UniformDistribution 的 PDF 与自身的卷积得到一个 TriangularDistribution:
UniformSumDistribution[n] 是 n 个 UniformDistribution[] 的概率密度函数的卷积:
ErlangDistribution[k,λ] 是 k 个 ExponentialDistribution[λ] 的概率密度函数的卷积:
属性和关系 (7)
Convolve 在实数线上计算一个积分:
与 DiracDelta 的卷积给出函数本身:
Wolfram Research (2008),Convolve,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Convolve.html.
文本
Wolfram Research (2008),Convolve,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Convolve.html.
CMS
Wolfram 语言. 2008. "Convolve." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/Convolve.html.
APA
Wolfram 语言. (2008). Convolve. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Convolve.html 年