HeavisidePi[x]
represents the box distribution ![]() , equal to 1 for
, equal to 1 for ![]() and 0 for
and 0 for ![]() .
.
HeavisidePi[x1,x2,…]
represents the multidimensional box distribution ![]() which is 1 if all
which is 1 if all ![]() .
.




HeavisidePi
HeavisidePi[x]
represents the box distribution ![]() , equal to 1 for
, equal to 1 for ![]() and 0 for
and 0 for ![]() .
.
HeavisidePi[x1,x2,…]
represents the multidimensional box distribution ![]() which is 1 if all
which is 1 if all ![]() .
.
Details
- HeavisidePi[x] returns 0 or 1 for all numeric x other than -1/2 and 1/2.
- HeavisidePi[x] is equivalent to HeavisideTheta[
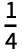 -x2].
-x2]. - HeavisidePi can be used in derivatives, integrals, integral transforms and differential equations.
- HeavisidePi has attribute Orderless.
Examples
open all close allBasic Examples (4)
The derivative generates DiracDelta distributions:
Scope (38)
Numerical Evaluation (6)
HeavisidePi always returns an exact result:
Evaluate efficiently at high precision:
HeavisidePi threads over lists:
Compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix HeavisidePi function using MatrixFunction:
Specific Values (4)
As a distribution, HeavisidePi does not have specific values at ![]() :
:
Find a value of x for which the HeavisidePi[x]=1:
Visualization (4)
Plot the HeavisidePi function:
Visualize scaled HeavisidePi functions:
Visualize the composition of HeavisidePi with a periodic function:
Plot HeavisidePi in three dimensions:
Function Properties (12)
Function domain of HeavisidePi:
It is restricted to real inputs:
Function range of HeavisidePi:
HeavisidePi is an even function:
The area under HeavisidePi is 1:
HeavisidePi has a jump discontinuity at the points ![]() :
:
HeavisidePi is not an analytic function:
It has both singularities and discontinuities:
HeavisidePi is neither nonincreasing nor nondecreasing:
HeavisidePi is not injective:
HeavisidePi is not surjective:
HeavisidePi is non-negative on its domain:
HeavisidePi is neither convex nor concave:
TraditionalForm formatting:
Differentiation (4)
Differentiate the univariate HeavisidePi:
Differentiate the multivariate HeavisidePi:
Higher derivatives with respect to z:
Differentiate a composition involving HeavisidePi:
Integration (4)
Integrate over finite domains:
Integrate over infinite domains:
Integrate expressions containing symbolic derivatives of HeavisidePi:
Integral Transforms (4)
The FourierTransform of a unit box is a Sinc function:
Find the LaplaceTransform of a unit box:
The convolution of HeavisidePi with itself is HeavisideLambda:
Applications (2)
Integrate a function involving HeavisidePi symbolically and numerically:
Solve an initial value problem for the heat equation:
Solve the initial value problem using ![]() :
:
Compare with the solution given by DSolveValue:
Properties & Relations (2)
The derivative of HeavisidePi is a distribution:
The derivative of UnitBox is a piecewise function:
HeavisidePi can be expressed in terms of HeavisideTheta:
See Also
Related Guides
Related Links
History
Text
Wolfram Research (2008), HeavisidePi, Wolfram Language function, https://reference.wolfram.com/language/ref/HeavisidePi.html.
CMS
Wolfram Language. 2008. "HeavisidePi." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HeavisidePi.html.
APA
Wolfram Language. (2008). HeavisidePi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeavisidePi.html
BibTeX
@misc{reference.wolfram_2025_heavisidepi, author="Wolfram Research", title="{HeavisidePi}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/HeavisidePi.html}", note=[Accessed: 16-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_heavisidepi, organization={Wolfram Research}, title={HeavisidePi}, year={2008}, url={https://reference.wolfram.com/language/ref/HeavisidePi.html}, note=[Accessed: 16-January-2026]}