GreenFunction

GreenFunction[{ℒ[u[x]],ℬ[u[x]]},u,{x,xmin,xmax},y]

gives a Green's function for the linear differential operator ℒ with boundary conditions ℬ in the range xmin to xmax.

GreenFunction[{ℒ[u[x1,x2,…]],ℬ[u[x1,x2,…]]},u,{x1,x2,…}∈Ω,{y1,y2,…}]

gives a Green's function for the linear partial differential operator ℒ over the region Ω.

GreenFunction[{ℒ[u[x,t]],ℬ[u[x,t]]},u,{x,xmin,xmax},t,{y,τ}]

gives a Green's function for the linear time-dependent operator ℒ in the range xmin to xmax.

GreenFunction[{ℒ[u[x1,…,t]],ℬ[u[x1,…,t]]},u,{x1,…}∈Ω,t,{y1,…,τ}]

gives a Green's function for the linear time-dependent operator ℒ over the region Ω.

Details and Options

  • GreenFunction represents the response of a system to an impulsive DiracDelta driving function.
  • GreenFunction for a differential operator 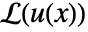is defined to be a solution 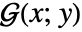of L(G(x;y))=TemplateBox[{{x, -, y}}, DiracDeltaSeq] that satisfies the given homogeneous boundary conditions .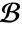
  • A particular solution of 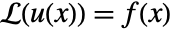with homogeneous boundary conditions 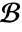can be obtained by performing a convolution integral .
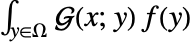  • GreenFunction for a time-dependent differential operator 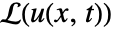is defined to be a solution 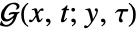of L(G(x,t;y,tau))=TemplateBox[{{x, -, y}}, DiracDeltaSeq]TemplateBox[{{t, -, tau}}, DiracDeltaSeq] that satisfies the given homogeneous boundary conditions .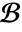
  • A particular solution of 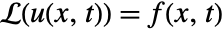with homogeneous boundary conditions 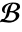can be obtained by performing a convolution integral .
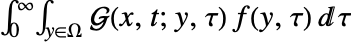  • The Green's functions for classical PDEs have characteristic geometrical properties:
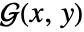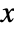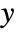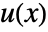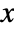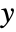  • is given as an expression in and if the dependent variable is of the form , and as a pure function with formal parameters and if the dependent variable is of the form 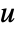instead of . »
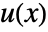  • The region Ω can be anything for which RegionQ[Ω] is True.
  • All the necessary initial and boundary conditions for ODEs must be specified in .
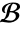  • Boundary conditions for PDEs must be specified using DirichletCondition or NeumannValue in .
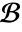  • Assumptions on parameters may be specified using the Assumptions option.

Examples

open allclose all

Basic Examples  (2)

Green's function for a boundary value problem:

Green's function for the heat operator on the real line:

Scope  (22)

Basic Uses  (2)

Compute the Green's function for an ordinary differential operator:

Obtain a pure function in the result by using u instead of u[x] in the second argument:

Compute the Green's function for a partial differential operator:

Obtain a pure function in the result by using u instead of u[x,t] in the second argument:

Ordinary Differential Equations  (4)

Compute the Green's function for an initial value problem:

Compute the Green's function for a Dirichlet problem:

Compute the Green's function for a Neumann problem:

Compute the Green's function for a Robin problem:

Wave Equation  (4)

Green's function for the wave operator on the real line:

Green's function for the wave operator with a Dirichlet condition on a half-line:

Green's function for the wave operator with a Neumann condition on a half-line:

Green's function for the wave operator with a Dirichlet condition on an interval:

Heat Equation  (5)

Green's function for the heat operator on the real line:

Green's function for the heat operator with a Dirichlet condition on a half-line:

Green's function for the heat operator with a Dirichlet condition on an interval:

Green's function for the heat operator with a Neumann condition on an interval:

Green's function for the heat operator in the plane:

Laplace Equation  (4)

Green's function for the Laplacian in two dimensions:

Dirichlet problem for the Laplacian in a quadrant of the plane:

Dirichlet problem for the Laplacian in a rectangle:

Green's function for the Laplacian in three dimensions:

Helmholtz Equation  (3)

Green's function for the Helmholtz operator in two dimensions:

Dirichlet problem for the Helmholtz operator in the upper half-plane:

Dirichlet problem for the Helmholtz operator in a rectangle:

Options  (1)

Assumptions  (1)

Specify Assumptions on parameters in GreenFunction:

Obtain a simpler result under the assumption that t>s:

Applications  (9)

Ordinary Differential Equations  (4)

Solve an initial value problem for an inhomogeneous differential equation using GreenFunction:

Define a forcing function:

Perform a convolution of the Green's function with the forcing function:

Compare with the result given by DSolveValue:

Solve a Dirichlet problem for an inhomogeneous differential equation using GreenFunction:

Define a forcing function:

Perform a convolution of the Green's function with the forcing function:

Compare with the result given by DSolveValue:

Solve a Neumann problem for an inhomogeneous differential equation using GreenFunction:

Define a forcing function:

Perform a convolution of the Green's function with the forcing function:

Compare with the result given by DSolveValue:

Solve a Robin problem for an inhomogeneous differential equation using GreenFunction:

Define a forcing function:

Perform a convolution of the Green's function with the forcing function:

Compare with the result given by DSolveValue:

Partial Differential Equations  (2)

Solve the inhomogeneous wave equation using GreenFunction:

Define the inhomogeneous term:

Solve the inhomogeneous equation using :

Compare with the solution given by DSolveValue:

Solve an initial value problem for the heat equation using GreenFunction:

Specify an initial value:

Solve the initial value problem using :

Compare with the solution given by DSolveValue:

Physics and Engineering  (3)

Compute the current i[t] in a circuit with a voltage source v[t] that is connected to a resistor R and an inductor L. The operator for this circuit is given by:

Diagram for the circuit:

Compute the Green's function:

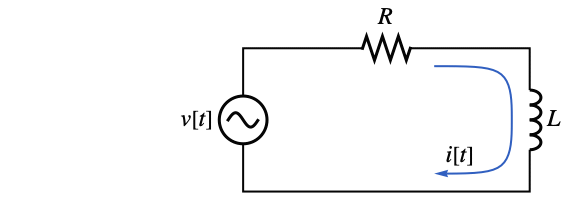
Find the current for a given voltage source:

Compute the displacement u[x] for a string of length p and tension T that is fixed at the two ends and is subjected to a force per unit length of f[x]. The operator for the displacement is given by:

Force diagram:

Compute the Green's function:

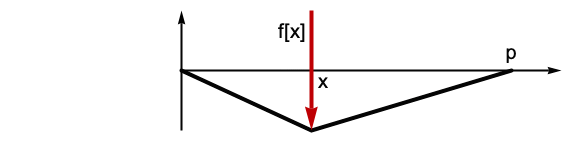
Find the displacement for a given force:

The impulse response of a continuous linear time-invariant system can be found by using the Green's function for the system with homogeneous initial conditions. Compute the impulse response for the system defined by:

Green's function for the system with homogeneous initial conditions:

Obtain the impulse response by setting s=0:

Plot the impulse response:

Properties & Relations  (2)

Compute a Green's function for a differential equation:

Obtain the same result using DSolve:

GreenFunction is related to OutputResponse and TransferFunctionModel:

Wolfram Research (2016), GreenFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/GreenFunction.html.

Text

Wolfram Research (2016), GreenFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/GreenFunction.html.

CMS

Wolfram Language. 2016. "GreenFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GreenFunction.html.

APA

Wolfram Language. (2016). GreenFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GreenFunction.html

BibTeX

@misc{reference.wolfram_2024_greenfunction, author="Wolfram Research", title="{GreenFunction}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/GreenFunction.html}", note=[Accessed: 17-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_greenfunction, organization={Wolfram Research}, title={GreenFunction}, year={2016}, url={https://reference.wolfram.com/language/ref/GreenFunction.html}, note=[Accessed: 17-December-2024 ]}