Laplacian
Details

- Laplacian is also known as Laplace–Beltrami operator. When applied to vector fields, it is also known as vector Laplacian.
- Laplacian[f,x] can be input as
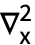 f. The character ∇ can be typed as
f. The character ∇ can be typed as  del
del or \[Del]. The list of variables x and the 2 are entered as a subscript and superscript, respectively.
or \[Del]. The list of variables x and the 2 are entered as a subscript and superscript, respectively. - An empty template
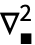 can be entered as
can be entered as  del2
del2 , and
, and  moves the cursor from the subscript to the main body.
moves the cursor from the subscript to the main body. - All quantities that do not explicitly depend on the variables given are taken to have zero partial derivative.
- Laplacian[f,{x1,x2,…}] yields a result with the same dimensions as f.
- In Laplacian[f,{x1,…,xn},chart], if f is an array, it must have dimensions {n,…,n}. The components of f are interpreted as being in the orthonormal basis associated to chart.
- For coordinate charts on Euclidean space, Laplacian[f,{x1,…,xn},chart] can be computed by transforming f to Cartesian coordinates, computing the ordinary Laplacian and transforming back to chart. »
- A property of Laplacian is that if chart is defined with metric g, expressed in the orthonormal basis, then Laplacian[g,{x1,…,xn},chart] gives zero. »
- Coordinate charts in the third argument of Laplacian can be specified as triples {coordsys,metric,dim} in the same way as in the first argument of CoordinateChartData. The short form in which dim is omitted may be used.
- Laplacian[f,VectorSymbol[…]] computes the Laplacian with respect to the vector symbol. »
- Laplacian works with SparseArray and structured array objects.
Examples
open all close allBasic Examples (4)
The Laplacian in three-dimensional Cartesian coordinates:
The Laplacian in three-dimensional cylindrical coordinates:
The Laplacian in two-dimensional polar coordinates:
Use ![]() del
del![]() to enter ∇,
to enter ∇, ![]() for the list of subscripted variables, and
for the list of subscripted variables, and ![]() to enter the 2:
to enter the 2:
Use ![]() del2
del2![]() to enter the template
to enter the template ![]() , fill in the variables, press
, fill in the variables, press ![]() , and fill in the function:
, and fill in the function:
Scope (6)
Laplacian applies to arrays of arbitrary rank:
In a curvilinear coordinate system, a vector with constant components may have a nonzero Laplacian:
A Laplacian specifying metric, coordinate system, and parameters:
Laplacian works on curved spaces:
The Laplacian of the coordinate vector is SymbolicZerosArray[{n}]:
The Laplacian of the squared norm is expressed in terms of SymbolicIdentityArray[{n}]:
Use TensorExpand to simplify to the expected result, namely twice the dimension:
Applications (3)
Poisson's equation in spherical coordinates:
Solve for a radially symmetric charge distribution ![]() :
:
The Laplacian on the unit sphere:
The spherical harmonics ![]() are eigenfunctions of this operator with eigenvalue
are eigenfunctions of this operator with eigenvalue ![]() :
:
The generalization of the Coulomb potential—the electric potential of a point charge—to n dimensions is:
Since the charge density is only nonzero at the origin, the Laplacian must be equal to zero everywhere else:
Activating the result in specific dimensions and combining denominators shows the result is zero:
This result can also be obtained in each dimension using spherical coordinates:
Properties & Relations (8)
Laplacian preserves the shape of an array:
The Laplacian is equal to the divergence of the gradient:
Since Grad uses an orthonormal basis, the Laplacian of a scalar equals the trace of the double gradient:
For higher-rank arrays, this is the contraction of the last two indices of the double gradient:
Compute Laplacian in a Euclidean coordinate chart c by transforming to and then back from Cartesian coordinates:
The result is the same as directly computing Laplacian[f,{x1,…,xn},c]:
The Laplacian of an array equals the Laplacian of its components only in Cartesian coordinates:
If chart is defined with metric g, expressed in the orthonormal basis, Laplacian[g,{x1,…,xn},chart] is zero:
For a vector field ![]() in three-dimensional flat space, the Laplacian is equal to
in three-dimensional flat space, the Laplacian is equal to ![]() :
:
In a flat space of dimension ![]() , the Laplacian of a vector field equals
, the Laplacian of a vector field equals ![]() . For
. For ![]() :
:
Laplacian preserves the symmetry structure of SymmetrizedArray objects:
See Also
Grad Div Curl CoordinateChartData D DSolve NDSolve DEigensystem NDEigensystem DEigenvalues NDEigenvalues
Characters: \[Del]
Tech Notes
Text
Wolfram Research (2012), Laplacian, Wolfram Language function, https://reference.wolfram.com/language/ref/Laplacian.html (updated 2024).
CMS
Wolfram Language. 2012. "Laplacian." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Laplacian.html.
APA
Wolfram Language. (2012). Laplacian. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Laplacian.html
BibTeX
@misc{reference.wolfram_2025_laplacian, author="Wolfram Research", title="{Laplacian}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Laplacian.html}", note=[Accessed: 06-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_laplacian, organization={Wolfram Research}, title={Laplacian}, year={2024}, url={https://reference.wolfram.com/language/ref/Laplacian.html}, note=[Accessed: 06-March-2026]}

