CoordinateChartData

CoordinateChartData[chart,property]

gives the value of the specified property for chart.

CoordinateChartData[chart,property,{x1,x2,…,xn}]

gives the value of the specified property for chart evaluated at the point {x1,x2,…,xn}.

Details

  • A coordinate chart may be specified by a coordinate system name, by a pair {coordsys,dim}, or by a standard name of the form {coordsys,metric,dim}. The dimension dim is a positive integer. Pairs {coordsys,dim} are interpreted as referring to the Euclidean metric.
  • Valid metric specifications include:
  • "metric"metric with default parameter values
    {"metric",param}metric with a single parameter specified
    {"metric",{param1,param2,…}}metric with several parameters specified
  • Valid coordinate system specifications include:
  • "coordsys"coordinate system with default parameter values
    {"coordsys",param}coordinate system with a single parameter specified
    {"coordsys",{param1,param2,…}}coordinate system with several parameters specified
  • If an evaluation point {x1,x2,…,xn} is given, the dimension n may be omitted from the coordinate chart name in the first argument.
  • Any or all of the elements of the triple in {coordsys,metric,dim} can be replaced with the symbol All. In this case, CoordinateChartData[chart,property] will return a list of values for the coordinate charts that match the specified elements.
  • CoordinateChartData[] gives a list of available coordinate charts, including only low-dimensional members of infinite families.
  • CoordinateChartData[chart] is equivalent to CoordinateChartData[chart,"StandardName"].
  • CoordinateChartData["Properties"] returns a list of available properties.
  • When no evaluation point {x1,x2,…,xn} is specified, properties are typically pure functions expecting a list of length n.
  • Basic properties include:
  • "AlternateCoordinateNames"common alternate coordinate names, as strings, used for the chart
    "CoordinateRangeAssumptions"logical expression for the assumptions satisfied by the coordinates of the chart
    "Dimension"dimension
    "ParameterRangeAssumptions"logical expression for the assumptions satisfied by the parameters of the chart
    "StandardCoordinateNames"the names, as strings, of the most common coordinate names used for the chart
    "StandardName"Wolfram Language standard name
  • Metric-related properties include:
  • "InverseMetric"components of the inverse (contravariant) metric tensor in the coordinated basis
    "Metric"components of the metric tensor in the coordinated basis
    "ScaleFactors"scale factors, as a list, of an orthogonal chart
    "VolumeFactor"coefficient of the differential in volume integrals
  • In Euclidean coordinate charts {coordsys,"Euclidean",n} with integer n, valid coordsys values include:
  • "Cartesian"Cartesian coordinates for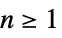
    "Hyperspherical"spherical coordinates with poles along the 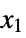axis for 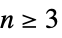, and polar coordinates for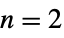
    {"Confocal", {α1,…,αn}}confocal coordinates with coordinates bounded from below in increasing order and semimajor axes 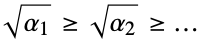for .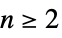
  • In two-dimensional Euclidean coordinate charts {coordsys,"Euclidean",2}, valid coordsys values include:
  • "Polar"polar coordinates
    {"Bipolar",{a}}bipolar coordinates with focal length 2a in the order focal angle, logarithmic radius
    {"Elliptic",{a}}elliptic coordinates with focal length 2a in the order hyperbolic radius, azimuthal angle
    "PlanarParabolic"two-dimensional parabolic coordinates
  • In three-dimensional Euclidean coordinate charts {coordsys,"Euclidean",3}, valid coordsys values include:
  • "Cylindrical"polar-cylindrical coordinates
    "Spherical"spherical coordinates with poles along the 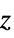axis and coordinates in the order radius, polar angle, azimuthal angle
    {"BipolarCylindrical",{a}}bipolar-cylindrical coordinates with focal length 2a in the order focal angle, logarithmic radius,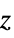
    {"Bispherical",{a}}bispherical coordinates with focal length 2a in the order focal angle, logarithmic radius, azimuthal angle
    "CircularParabolic"parabolic coordinates with the last coordinate azimuthal angle
    {"ConfocalParaboloidal", {α,β}}confocal paraboloidal coordinates on the 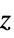axis with foci 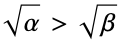, coordinates positive in increasing order
    {"Conical",{b,c}}conical coordinates with parameters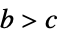
    {"EllipticCylindrical", {a}}elliptic-cylindrical coordinates with focal length 2a in the order hyperbolic radius, azimuthal angle,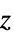
    {"OblateSpheroidal",{a}}oblate spheroidal coordinates with focal length 2a in the order hyperbolic radius, polar angle, azimuthal angle
    "ParabolicCylindrical"parabolic-cylindrical coordinates
    {"ProlateSpheroidal",{a}}prolate spheroidal coordinates with focal length 2a in the order hyperbolic radius, polar angle, azimuthal angle
    {"Toroidal",a}toroidal coordinates with ring radius 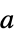in the order logarithmic radius, focal angle, azimuthal angle
  • In coordinate charts {coordsys,"Sphere",n} on the 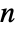-sphere, valid coordsys values include:
  • "Standard"standard angular coordinates
    "Stereographic"
  • stereographic projection onto the 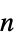-plane

Examples

open allclose all

Basic Examples  (1)

Three-dimensional spherical coordinates:

Scope  (22)

Names  (7)

CoordinateChartData[] returns a list of available charts, including only low-dimensional members of infinite families:

Pairs {coordsys,dim} are equivalent to {coordsys,"Euclidean",dim}:

When an evaluation point is given, the dimension may be omitted from the first argument:

Some special coordinate charts for the Euclidean metric can be entered using only the coordinate system name:

List all known three-dimensional coordinate systems in flat space:

Pairs {chart,dim} are equivalent to {chart,"Euclidean",dim}:

All available two-dimensional coordinate systems:

For infinite families, low-dimensional representatives are returned:

Specifying parameters may restrict relevant dimensions:

If no charts match, an empty list is returned:

Properties  (2)

Get a list of possible properties:

Give the scale factors for a single chart:

Retrieve all two-dimensional coordinate systems in flat space:

Give the corresponding scale factors:

Property Values  (2)

A property value can be any valid Wolfram Language expression:

For most properties, if no evaluation point is given, then CoordinateChartData will return a pure function:

This function can be applied to points:

Certain descriptive properties, which manifestly do not depend on the variables, never return a pure function as a property value:

The properties for which this happens include "Dimension", "ParameterRangeAssumptions", "StandardName", "StandardCoordinateNames", and "AlternateCoordinateNames".

Detailed Properties  (11)

Basic Properties  (7)

In general, coordinate charts are referred to by standard name:

That is equivalent to this simpler syntax:

Look up the coordinate chart dimension without doing pattern matching on the chart name:

Give assumptions for the range of polar coordinates:

Assumptions are returned in a form usable by Simplify and other functions that accept Assumptions:

Use "CoordinateRangeAssumptions" without specifying a point to create a test for point validity:

This is a valid point in spherical coordinates:

These are not valid points in spherical coordinates:

Give the assumptions for the parameter in prolate spheroidal coordinates:

Test that a particular value of the parameter is valid:

A message is issued and CoordinateChartData returns unevaluated if a value of the parameter violating the assumptions is used:

Look up the standard coordinate names used in spherical coordinates:

The names are given as strings:

Use ToExpression to convert them to symbols:

Look up common alternate coordinate names used in spherical coordinates:

The names are strings:

Use ToExpression to convert them to symbols:

Metric-Related Properties  (4)

Give the components of the (covariant) metric as a matrix:

By particularizing to a curve, the metric can be used to compute the differential arc length:

Give the components of the inverse (contravariant) metric as a matrix:

The inverse metric with a particular value of the parameter a:

Give the scale factors as a flat list:

In an orthogonal coordinate system, the scale factors relate the scalar gradient to partial differentiation:

Give the coefficient of the differential in spherical coordinates:

Find the volume of a region:

The volume is an -dimensional volume. For example, in two dimensions it corresponds to area:

Applications  (1)

A function to compute the differential arc length of a curve in a particular coordinate system:

The differential arc length of a general curve in polar coordinates:

The differential arc length of a helix expressed in cylindrical coordinates:

This can now be integrated:

Properties & Relations  (1)

CoordinateChartData checks that inputs obey the coordinate range assumptions of charts:

Extract the general formula using the two-argument form and apply it to extend to singular points:

Interactive Examples  (1)

Create an interactive table of Laplacian expressions in two-dimensional coordinate systems:

Wolfram Research (2012), CoordinateChartData, Wolfram Language function, https://reference.wolfram.com/language/ref/CoordinateChartData.html (updated 2014).

Text

Wolfram Research (2012), CoordinateChartData, Wolfram Language function, https://reference.wolfram.com/language/ref/CoordinateChartData.html (updated 2014).

CMS

Wolfram Language. 2012. "CoordinateChartData." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/CoordinateChartData.html.

APA

Wolfram Language. (2012). CoordinateChartData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoordinateChartData.html

BibTeX

@misc{reference.wolfram_2024_coordinatechartdata, author="Wolfram Research", title="{CoordinateChartData}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/CoordinateChartData.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_coordinatechartdata, organization={Wolfram Research}, title={CoordinateChartData}, year={2014}, url={https://reference.wolfram.com/language/ref/CoordinateChartData.html}, note=[Accessed: 22-December-2024 ]}