BilateralLaplaceTransform

BilateralLaplaceTransform[expr,t,s]

gives the bilateral Laplace transform of expr.

BilateralLaplaceTransform[expr,{t1,t2,…,tn},{s1,s2,…,sn}]

gives the multidimensional bilateral Laplace transform of expr.

Details and Options

  • The bilateral Laplace transform of a function 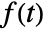is defined to be .
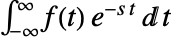  • The multidimensional bilateral Laplace transform is given by .
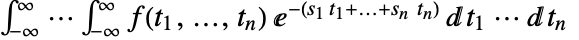  • The integral is computed using numerical methods if the third argument, s, is given a numerical value.
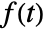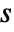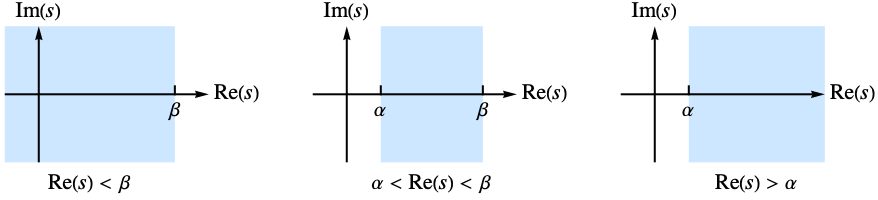
  • The bilateral Laplace transform of exists only for complex values of such that 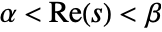. In some cases, this strip of definition may extend to a half-plane.
  • The following options can be given:
  • AccuracyGoalAutomaticdigits of absolute accuracy sought
    Assumptions $Assumptionsassumptions to make about parameters
    GenerateConditions Truewhether to generate answers that involve conditions on parameters
    MethodAutomaticmethod to use
    PerformanceGoal$PerformanceGoalaspects of performance to optimize
    PrecisionGoalAutomaticdigits of precision sought
    PrincipalValue Falsewhether to find Cauchy principal value
    WorkingPrecision Automaticthe precision used in internal computations

Examples

open allclose all

Basic Examples  (2)

Define an exponentially decaying function on the real line:

Compute its bilateral Laplace transform:

Complex plot of the bilateral Laplace transform:

Compute the transform at a single point:

Compute the bilateral Laplace transform of a multivariate function:

Scope  (20)

Univariate Functions  (8)

Bilateral Laplace transform of the UnitStep function:

Bilateral Laplace transform of the UnitBox function:

UnitTriangle function:

Power function:

Exponential function:

DiracDelta:

Piecewise function:

Product of a cosine and an exponential function:

Complex plot of the bilateral Laplace transform:

Multivariate Functions  (2)

Bilateral Laplace transform of a multivariate function:

Multivariate piecewise function:

Numerical Evaluation  (2)

Calculate the bilateral Laplace transform at a single point:

Alternatively, calculate the Laplace transform symbolically:

Then evaluate it for a specific value of :

For some functions, the bilateral Laplace transform can be evaluated only numerically:

Plot the bilateral Laplace transform using numerical values only:

Formal Properties  (8)

BilateralLaplaceTransform is a linear operator:

Bilateral Laplace transform of is the Laplace transform of evaluated at :

Scaling:

Time shifting:

Convolution property of the bilateral Laplace transform:

Differentiation in the time domain:

Multiplication of the function by t with a positive integer power:

Integration in the time domain:

Options  (4)

Assumptions  (1)

Specify the range for a parameter using Assumptions:

GenerateConditions  (1)

Set GenerateConditions to False to obtain a result without conditions:

PrincipalValue  (1)

The bilateral transform of the following function is not defined due to the singularity at :

Use PrincipalValue to obtain the Cauchy principal value for the integral:

WorkingPrecision  (1)

Use WorkingPrecision to obtain a result with arbitrary precision:

Properties & Relations  (2)

BilateralLaplaceTransform and InverseBilateralLaplaceTransform are mutual inverses:

Use NIntegrate to obtain a numerical approximation:

NIntegrate computes the transform for numeric values of the bilateral Laplace parameter s:

Neat Examples  (1)

Create a table of basic bilateral Laplace transforms:

Wolfram Research (2021), BilateralLaplaceTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/BilateralLaplaceTransform.html.

Text

Wolfram Research (2021), BilateralLaplaceTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/BilateralLaplaceTransform.html.

CMS

Wolfram Language. 2021. "BilateralLaplaceTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BilateralLaplaceTransform.html.

APA

Wolfram Language. (2021). BilateralLaplaceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BilateralLaplaceTransform.html

BibTeX

@misc{reference.wolfram_2025_bilaterallaplacetransform, author="Wolfram Research", title="{BilateralLaplaceTransform}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/BilateralLaplaceTransform.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_bilaterallaplacetransform, organization={Wolfram Research}, title={BilateralLaplaceTransform}, year={2021}, url={https://reference.wolfram.com/language/ref/BilateralLaplaceTransform.html}, note=[Accessed: 21-February-2025 ]}