TruncateSum

TruncateSum[sexpr,n]

truncates each Sum in sexpr to have at most n terms.

TruncateSum[sexpr,{m,n,…}]

truncates each multiple Sum in sexpr using the iterative specification {m,n,…}.

Details and Options

TruncateSum is typically used to truncate symbolic solutions involving infinite sums to finite sums, making it easy to numerically evaluate such approximations.

The sum expression sexpr can have any combination of unevaluated and Inactive sums.
TruncateSum will truncate large positive or negative summation limits according to the following:
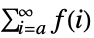
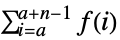
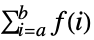
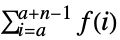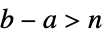
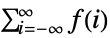
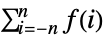
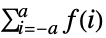
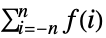, if

, if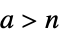
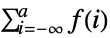
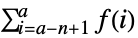
The following options can be given:
ActivateResult True whether to Activate the result

WorkingPrecision Automatic the precision used in internal computations

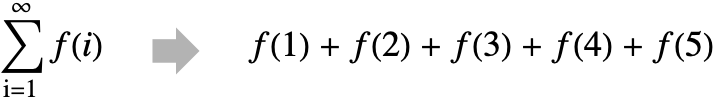
Examples

open allclose all

Basic Examples (2)

Truncate an infinite sum to its first 12 terms:

Truncate an inactive sum:

Avoid activating the inactive sum:

Activate the result:

Scope (13)

Basic Uses (3)

Truncate an infinite sum to its first 10 terms:

Truncate an infinite sum to a sum with a symbolic upper limit:

For unevaluated sums, TruncateSum directly evaluates the truncated sum:

Finite Sums (3)

Truncate a finite sum:

Truncate a sum with symbolic upper limit:

Truncate a sum with symmetric upper and lower limits:

Infinite Sums (4)

Truncate an infinite sum:

Truncate a sum with doubly infinite limits:

Truncate a sum with –∞ as its lower limit:

Truncate a polynomial with infinite sum coefficients:

Multiple Sums (2)

Truncate a doubly infinite sum:

Specify the maximum number of total terms for each sum:

Truncate only the first sum:

Truncate only the second sum:

Truncate a double sum:

Specify the maximum number of individual terms:

Inactive Sums (1)

For inactive sums, TruncateSum tries to evaluate the truncated sum:

Use ActivateResultFalse to avoid activating the inactive sum:

Activate the result:

Options (1)

WorkingPrecision (1)

Truncate a double sum:

Truncate the sum using 20-digit precision arithmetic:

Applications (10)

Differential Equations (4)

Solve the Dirichlet problem for the wave equation on a finite interval:

The solution is an infinite trigonometric series:

Extract the first three terms from the Inactive sum:

Solve the Dirichlet problem for the wave equation in a rectangle:

The solution is a doubly infinite trigonometric series:

Extract a few terms from the Inactive sums:

Solve the Dirichlet problem for the heat equation on a finite interval:

The solution is a Fourier sine series:

Truncate the Inactive sum:

Solve the initial value problem for a Schrödinger equation with Dirichlet boundary conditions:

Define a family of partial sums of the solution:

For each k, u_k satisfies the differential equation:

The boundary conditions are also satisfied:

The initial condition is only satisfied for u_∞, but there is rapid convergence at t==2:

Difference Equations (1)

Solve a difference equation:

Extract the solution for :

Asymptotics (3)

Compute the power series expansion of around 0:

Obtain the first seven nonzero terms in the series:

Compute the power series expansion of around 1:

Obtain the first five terms in the series:

Truncate the series for the Hypergeometric1F1 function:

Compare the results with the built-in Hypergeometric1F1 function:

Inverse Laplace Transform (2)

Calculate the inverse Laplace transform of a function:

Truncate the sum and plot the result:

The inverse Laplace transform of this function is a piecewise function:

Truncate and plot the result:

Properties & Relations (4)

TruncateSum[expr,n] truncates each sum in the expression to have at most n terms:

TruncateSum truncates both limits of doubly infinite sums:

TruncateSum truncates only the lower limit of a sum from –∞ to a finite value:

TruncateSum activates all inactive sums in the expression:

ActivateResult False can be used to avoid activation:

Possible Issues (1)

The number of terms in the truncated sum is assumed to be an integer:

Top

TruncateSum

Details and Options

Examples

Basic Examples (2)