FourierCosTransform

FourierCosTransform[expr,t,ω]

gives the symbolic Fourier cosine transform of expr.

FourierCosTransform[expr,{t₁,t₂,…},{ω₁,ω₂,…}]

gives the multidimensional Fourier cosine transform of expr.

Details and Options

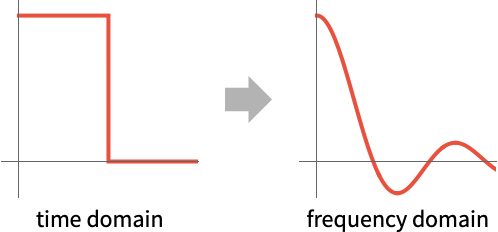
The Fourier cosine transform is a particular way of viewing the Fourier transform without the need for complex numbers or negative frequencies.
Joseph Fourier designed his famous transform using this and the Fourier sine transform, and they are still used in applications like signal processing, statistics and image and video compression.
The Fourier cosine transform of the time domain function 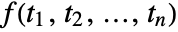is the frequency domain function 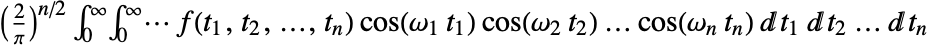for :

The Fourier cosine transform of a function 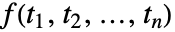is by default defined to be .
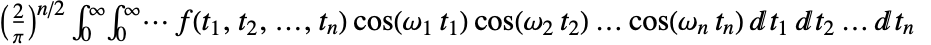The multidimensional Fourier cosine transform of a function 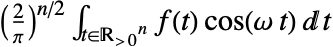is by default defined to be or when using vector notation, $(2/pi)^(n/2)int_(t in TemplateBox[{}, PositiveReals]^n) f(t) cos(omega t)dt$ .
Different choices of definitions can be specified using the option FourierParameters.
The integral is computed using numerical methods if the third argument, , is given a numerical value.
The asymptotic Fourier cosine transform can be computed using Asymptotic.
There are several related Fourier transformations:

	FourierTransform	infinite continuous-time functions (FT)
	FourierSequenceTransform	infinite discrete-time functions (DTFT)
	FourierCoefficient	finite continuous-time functions (FS)
	Fourier	finite discrete-time functions (DFT)

The Fourier cosine transform is an automorphism in the Schwartz vector space of functions whose derivatives are rapidly decreasing and thus induces an automorphism in its dual: the space of tempered distributions. These include absolutely integrable functions, well-behaved functions of polynomial growth and compactly supported distributions.
Hence, FourierCosTransform not only works with absolutely integrable functions on , but it can also handle a variety of tempered distributions such as DiracDelta to enlarge the pool of functions or generalized functions it can effectively transform.
The lower limit of the integral is effectively taken to be , so that the Fourier cosine transform of the Dirac delta function 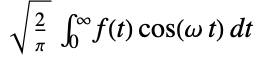is equal to . »
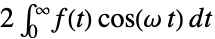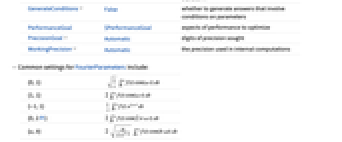
The following options can be given:

AccuracyGoal	Automatic	digits of absolute accuracy sought
Assumptions	$Assumptions	assumptions to make about parameters
FourierParameters	{0,1}	parameters to define the Fourier cosine transform
GenerateConditions	False	whether to generate answers that involve conditions on parameters
PerformanceGoal	$PerformanceGoal	aspects of performance to optimize
PrecisionGoal	Automatic	digits of precision sought
WorkingPrecision	Automatic	the precision used in internal computations

Common settings for FourierParameters include:
{0,1}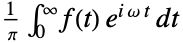

{1,1}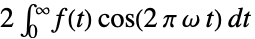

{-1,1}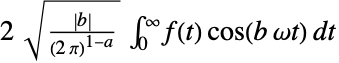

{0,2Pi}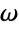

{a,b}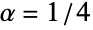

Examples

open allclose all

Basic Examples (6)

Compute the Fourier cosine transform of a function:

Plot the function and its Fourier cosine transform:

Fourier cosine transform of reciprocal square root:

For a different convention, change the parameters:

Fourier cosine transform of a Gaussian is another Gaussian:

Plot both Gaussians:

Compute the Fourier cosine transform of a multivariate function:

Plot the result:

Compute the transform at a single point:

Scope (39)

Basic Uses (3)

Fourier cosine transform of a function for a symbolic parameter :

Fourier cosine transforms involving trigonometric functions:

Plot the transform:

Plot the transform for :

Evaluate the Fourier cosine transform for a numerical value of the parameter :

Algebraic Functions (4)

Fourier cosine transform of power functions:

Cosine transform for rational functions:

Plot the transform:

Fourier cosine transform of a quotient of two nonlinear polynomials:

Plot the transform:

Fourier cosine transform of a quotient of quadratic and quartic polynomials:

Plot the transform:

Exponential and Logarithmic Functions (3)

Fourier cosine transform of an exponential function:

Transform for :

Plot the transform:

Fourier cosine transforms of products of exponential and trigonometric functions:

Plot the transform for and :

Plot the transform:

Cosine transforms of logarithmic functions:

Plot the transform:

Trigonometric Functions (5)

Expressions involving trigonometric functions:

Plot the transform:

Composition of elementary functions:

Plot the transform for :

Ratio of sine and product of exponential and linear functions:

Plot the transform:

Fourier cosine transform of arctangent functions:

Plot the transform:

Fourier cosine transform of Sech is another Sech:

Plot the transform:

Special Functions (7)

Sinc function:

Plot the transform:

Fourier cosine transforms of expressions involving ExpIntegralEi:

Plot the transform:

Expression involving Erfc:

Plot the transform for :

Expression involving SinIntegral:

Plot the transform:

CosIntegral:

Plot the transform:

Cosine transforms for BesselJ functions:

Plot the transform for :

Plot the transform for and :

Plot the transform:

Cosine transforms for BesselY functions:

Plot the transform for :

Plot the transform for and :

Piecewise Functions and Distributions (4)

Fourier cosine transform of a piecewise function:

Restriction of a sine function to a half-period:

Triangular function:

Transforms in terms of FresnelC:

Plot the transform:

Periodic Functions (2)

Fourier cosine transform of cosine:

Fourier cosine transform of SquareWave:

Generalized Functions (4)

Fourier cosine transforms of expressions involving HeavisideTheta:

Fourier cosine transforms involving DiracDelta:

Plot the transform:

Fourier cosine transform involving HeavisideLambda:

Fourier cosine transform involving HeavisidePi:

Multivariate Functions (2)

Fourier cosine transforms of exponentials in two variables:

Plot of both:

Fourier cosine transform of product of exponential and SquareWave:

Formal Properties (3)

Fourier cosine transform of a first-order derivative:

Fourier cosine transform of a second-order derivative:

Fourier cosine transform threads itself over equations:

Numerical Evaluation (2)

Calculate the Fourier cosine transform at a single point:

Alternatively, calculate the Fourier cosine transform symbolically:

Then evaluate it for specific value of :

Options (8)

AccuracyGoal (1)

The option AccuracyGoal sets the number of digits of accuracy:

With default settings:

Assumptions (1)

Fourier cosine transform of BesselJ is a piecewise function:

FourierParameters (3)

Fourier cosine transform for the unit box function with different parameters:

Use a nondefault setting for a different definition of transform:

To get the inverse, use the same FourierParameters setting:

Set up your particular global choice of parameters once per session:

Restore defaults:

GenerateConditions (1)

Use GenerateConditionsTrue to get parameter conditions for when a result is valid:

PrecisionGoal (1)

The option PrecisionGoal sets the relative tolerance in the integration:

With default settings:

WorkingPrecision (1)

If a WorkingPrecision is specified, the computation is done at that working precision:

With default settings:

Applications (4)

Ordinary Differential Equations (1)

Consider the following ODE with initial condition :

Apply the Fourier cosine transform to the ODE:

Solve for the Fourier cosine transform of :

Find the inverse Fourier cosine transform with and :

Compare with DSolveValue:

Partial Differential Equations (1)

Solve the heat equation for , : with initial condition for and Neumann boundary condition for .

Apply the Fourier cosine transform to the ODE on :

With and , solve this ODE:

Compute the inverse cosine transform of the exponential functions:

The convolution property gives the inverse cosine transform of the first summand to get the solution:

Consider the special case with , and :

Compare with DSolveValue:

Plot the initial conditions and solutions for different values of .

Evaluation of Integrals (2)

Calculate the following definite integral:

Fourier cosine transform preserves integration of products over :

Solve the definite integral:

Compare with Integrate:

Calculate the following definite integral for :

Compute Fourier cosine transform of an exponential function:

Apply Parseval's identity:

Or equivalently:

Solve for the definite integral:

Compare with Integrate:

Properties & Relations (4)

By default, the Fourier cosine transform of is:

For , the definite integral becomes:

Compare with FourierCosTransform:

Use Asymptotic to compute an asymptotic approximation:

FourierCosTransform and InverseFourierCosTransform are mutual inverses:

Results from FourierCosTransform and FourierTransform agree for even functions:

The results agree for :

Possible Issues (1)

The result from an inverse Fourier cosine transform may not have the same form as the original:

Fourier cosine transform may be given in terms of generalized functions such as DiracDelta:

Neat Examples (2)

Fourier cosine transform as a Meijer function:

Create a table of basic Fourier cosine transforms:

Top

	{0,1}
	{1,1}
	{-1,1}
	{0,2Pi}
	{a,b}

FourierCosTransform

Details and Options

Examples

Basic Examples (6)

Scope (39)

Basic Uses (3)

Algebraic Functions (4)

Exponential and Logarithmic Functions (3)

Trigonometric Functions (5)

Special Functions (7)

Piecewise Functions and Distributions (4)

Periodic Functions (2)

Generalized Functions (4)

Multivariate Functions (2)

Formal Properties (3)

Numerical Evaluation (2)

Options (8)

AccuracyGoal (1)

Assumptions (1)

FourierParameters (3)

GenerateConditions (1)

PrecisionGoal (1)

WorkingPrecision (1)

Applications (4)

Ordinary Differential Equations (1)

Partial Differential Equations (1)

Evaluation of Integrals (2)

Properties & Relations (4)

Possible Issues (1)

Neat Examples (2)

See Also

Tech Notes

Related Guides

History

Text

CMS

APA

BibTeX

BibLaTeX