PowerSpectralDensity[data,ω]
estimates the power spectral density for data.
PowerSpectralDensity[data,ω,sspec]
estimates the power spectral density for data with smoothing specification sspec.
PowerSpectralDensity[tproc,ω]
represents the power spectral density of a time series process tproc.


PowerSpectralDensity
PowerSpectralDensity[data,ω]
estimates the power spectral density for data.
PowerSpectralDensity[data,ω,sspec]
estimates the power spectral density for data with smoothing specification sspec.
PowerSpectralDensity[tproc,ω]
represents the power spectral density of a time series process tproc.
Details and Options

- PowerSpectralDensity is also known as the energy spectral density.
- PowerSpectralDensity[tproc,ω] is defined for weakly stationary time series processes as
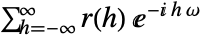 , where
, where 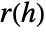 denotes CovarianceFunction[proc,h].
denotes CovarianceFunction[proc,h]. - The following smoothing specifications sspec can be given:
-
c use c as a cutoff w use a window function w {c,w} use both a cutoff and a window function - For a window function w and positive integer c, PowerSpectralDensity[data,ω,{c,w}] is computed as
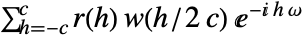 , where
, where 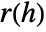 is defined as CovarianceFunction[data,h].
is defined as CovarianceFunction[data,h]. - By default, the cutoff c is chosen to be
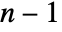 , where
, where 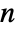 is the length of data, and the window function is DirichletWindow.
is the length of data, and the window function is DirichletWindow. - A window function
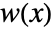 is an even function such that
is an even function such that 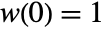 ,
, ![TemplateBox[{{w, (, x, )}}, Abs]<=1 TemplateBox[{{w, (, x, )}}, Abs]<=1](Files/PowerSpectralDensity.en/9.png) ,
, 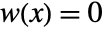 for
for ![TemplateBox[{x}, Abs]>1/2 TemplateBox[{x}, Abs]>1/2](Files/PowerSpectralDensity.en/11.png) , including standard windows such as HammingWindow, ParzenWindow, etc.
, including standard windows such as HammingWindow, ParzenWindow, etc. - A window function can be given as a list of values {w0,…}, where
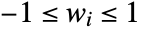 , and it will be applied symmetrically in the vector case.
, and it will be applied symmetrically in the vector case. - PowerSpectralDensity takes the FourierParameters option. Common settings for FourierParameters include:
-
{1,1} 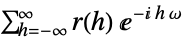
default setting {-1,1} 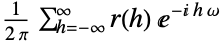
often used for time series {a,b} 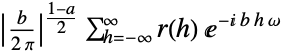
general setting
Examples
open all close allBasic Examples (3)
Scope (14)
Empirical Estimates (4)
Estimate the power spectral density for a univariate time series:
Power spectral density for a vector time series:
Power spectral density for each component:
Cross power spectral density between components:
Estimate the power spectral density for an ensemble of paths:
Compare empirical and theoretical power spectral densities functions:
Smoothing (5)
Obtain a smoothed estimate using a cutoff at 5:
Compare the smoothed spectrum to the original:
Compute the power spectral density using a NuttallWindow:
Compare the smoothed spectrum to the original:
Define a window using a pure function:
Compare the smoothed spectrum to the original:
Estimate the power spectral density using specified window function values:
Compare to power spectral density with explicit TukeyWindow:
Compare the smoothed spectrum to the original:
Compute the power spectral density, given a cutoff and a window function:
Random Processes (5)
Power spectral density for an ARProcess:
Vector ARProcess:
Power spectral density for an MAProcess:
Vector MAProcess:
Power spectral density for an ARMAProcess:
Vector ARMAProcess:
Power spectral density for a fractionally integrated time series:
Vector FARIMAProcess:
Power spectral density for a seasonal time series:
Vector SARMAProcess:
Options (2)
Applications (1)
Properties & Relations (11)
Power spectral density of a time series is a transform of the CovarianceFunction:
Compare to the power spectrum:
Power spectral density of data is a transform of the sample CovarianceFunction:
Apply ListFourierSequenceTransform:
Compare to SamplePowerSpectralDensity:
For a vector values time series:
Power spectrum of white noise:
Compare to special case of an MAProcess:
Integrate to find the variance:
Compare to the variance of the time series:
Integrate to find the sample second moment:
Compare to the sample second moment:
Power spectral density for harmonic frequencies is related to PeriodogramArray:
Compare with PeriodogramArray:
Diagonal elements of the power spectral density for vector data:
Compare to univariate power spectral density for each data component:
Power spectral density of a vector process is conjugate symmetric about zero:
Power spectral density of a univariate process is symmetric about zero:
Power spectral density of a vector process is Hermitian:
The magnitude of the sample cross spectral density is given by each component:
The determinant of the sample power spectral density is constant equal to zero:
Use TransferFunctionModel to calculate PowerSpectralDensity of a time series:
See Also
PeriodogramArray AbsoluteCorrelationFunction CovarianceFunction FourierSequenceTransform WeakStationarity ARMAProcess SARIMAProcess
Function Repository: WelchSpectralEstimate
Related Guides
Related Links
History
Text
Wolfram Research (2012), PowerSpectralDensity, Wolfram Language function, https://reference.wolfram.com/language/ref/PowerSpectralDensity.html.
CMS
Wolfram Language. 2012. "PowerSpectralDensity." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PowerSpectralDensity.html.
APA
Wolfram Language. (2012). PowerSpectralDensity. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PowerSpectralDensity.html
BibTeX
@misc{reference.wolfram_2025_powerspectraldensity, author="Wolfram Research", title="{PowerSpectralDensity}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/PowerSpectralDensity.html}", note=[Accessed: 26-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_powerspectraldensity, organization={Wolfram Research}, title={PowerSpectralDensity}, year={2012}, url={https://reference.wolfram.com/language/ref/PowerSpectralDensity.html}, note=[Accessed: 26-February-2026]}