FARIMAProcess[{a1,…,ap},d,{b1,…,bq},v]
represents an autoregressive fractionally integrated moving-average process ![]() such that its d
such that its d![]() difference is an ARMAProcess[{a1,…,ap},{b1,…,bq},v].
difference is an ARMAProcess[{a1,…,ap},{b1,…,bq},v].
FARIMAProcess[{a1,…,ap},d,{b1,…,bq},Σ]
represents a vector autoregressive fractionally integrated moving-average process (y1(t),… ,yn(t)) such that its (d,…,d)![]() difference is a vector ARMAProcess.
difference is a vector ARMAProcess.
FARIMAProcess[{a1,…,ap},{d1,…,dn},{b1,…,bq},Σ]
represents a vector autoregressive fractionally integrated moving-average process (y1(t),… ,yn(t)) such that its (d1,…,dn)![]() difference is a vector ARMAProcess.
difference is a vector ARMAProcess.


FARIMAProcess
FARIMAProcess[{a1,…,ap},d,{b1,…,bq},v]
represents an autoregressive fractionally integrated moving-average process ![]() such that its d
such that its d![]() difference is an ARMAProcess[{a1,…,ap},{b1,…,bq},v].
difference is an ARMAProcess[{a1,…,ap},{b1,…,bq},v].
FARIMAProcess[{a1,…,ap},d,{b1,…,bq},Σ]
represents a vector autoregressive fractionally integrated moving-average process (y1(t),… ,yn(t)) such that its (d,…,d)![]() difference is a vector ARMAProcess.
difference is a vector ARMAProcess.
FARIMAProcess[{a1,…,ap},{d1,…,dn},{b1,…,bq},Σ]
represents a vector autoregressive fractionally integrated moving-average process (y1(t),… ,yn(t)) such that its (d1,…,dn)![]() difference is a vector ARMAProcess.
difference is a vector ARMAProcess.
Details

- FARIMAProcess is also known as ARFIMA or long-memory time series.
- FARIMAProcess is a discrete-time and continuous-state random process.
- The FARIMA process is described by the difference equations
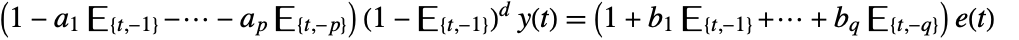 , where
, where 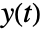 is the state output,
is the state output, 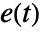 is the white noise input, and
is the white noise input, and 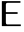 is the shift operator.
is the shift operator. - The scalar FARIMA process has transfer function
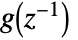 , where
, where 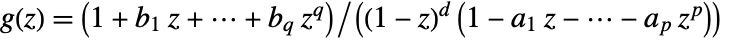 .
. - The vector FARIMA process has transfer matrix
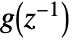 , where
, where 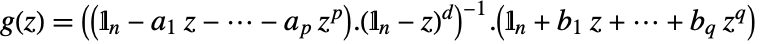 , and where
, and where 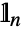 is the
is the 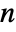 ×
×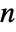 identity matrix.
identity matrix. - A scalar FARIMA process should have real coefficients ai, bj, real integrating parameter d such that
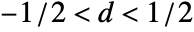 , and a positive variance v.
, and a positive variance v. - An
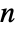 -dimensional vector FARIMA process should have real coefficient matrices ai and bj of dimensions
-dimensional vector FARIMA process should have real coefficient matrices ai and bj of dimensions 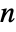 ×
×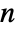 , real integrating parameters di such that
, real integrating parameters di such that 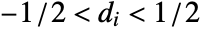 or real integrating parameter d such that
or real integrating parameter d such that 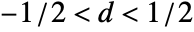 , and the covariance matrix Σ should be symmetric positive definite of dimensions
, and the covariance matrix Σ should be symmetric positive definite of dimensions 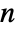 ×
×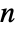 .
. - FARIMAProcess[p,d,q] and FARIMAProcess[p,q] represent a FARIMA process of orders p and q with known or unknown integration order d for use in EstimatedProcess and related functions.
- FARIMAProcess can be used with such functions as CovarianceFunction, RandomFunction, and TimeSeriesForecast.
Examples
open all close allBasic Examples (3)
Scope (25)
Basic Uses (8)
Simulate an ensemble of paths:
Simulate with given precision:
Simulate a first-order scalar process:
Sample paths for positive and negative values of the integration parameter:
Simulate a two-dimensional process:
Create a 2D sample path function from the data:
The color of the path is the function of time:
Create a 3D sample path function with time:
The color of the path is the function of time:
Simulate a three-dimensional process:
Create a sample path function from the data:
The color of the path is the function of time:
Compare the sample covariance function with that of the estimated process:
Estimate integration order of the fractional noise:
Compare the sample correlation function with that of the estimated process:
Covariance and Spectrum (5)
Closed-form correlation function for pure FARIMA:
For FARIMA with autoregressive and moving-average components available numerically:
Partial correlation has closed form for special case:
Vector FARIMAProcess:
Stationarity and Invertibility (4)
Estimation Methods (2)
The available methods for estimating a FARIMAProcess:
The available methods for estimating fractional noise:
Spectral estimator allows you to specify windows used for PowerSpectralDensity calculation:
Spectral estimator allows the following solvers:
Process Slice Properties (5)
Single time SliceDistribution:
Multiple time slice distributions:
First-order probability density function:
Compare with the density function of a normal distribution:
Compute the expectation of an expression:
Moment of order r:
CentralMoment and its generating function:
FactorialMoment has no closed form for symbolic order:
Cumulant and its generating function:
Representations (1)
Approximate with an ARMAProcess:
Approximate with an MAProcess:
Approximate with an ARProcess:
Compare random samples of the process and its approximation:
Applications (1)
Properties & Relations (5)
The correlations are summable for -1/2<d<0:
For 0<d<1/2, the sum of correlations diverges:
FARIMAProcess has a long memory for positive integration orders:
FARIMAProcess is a generalization of an ARMAProcess:
FARIMAProcess is a generalization of an ARProcess:
FARIMAProcess is a generalization of an MAProcess:
Possible Issues (2)
ToInvertibleTimeSeries does not always exist:
Method of moments is only supported for estimation of fractional noise:
Neat Examples (2)
Simulate a three-dimensional FARIMAProcess:
Simulate paths from a FARIMA process:
Take a slice at 50 and visualize its distribution:
Plot paths and histogram distribution of the slice distribution at 50:
Related Guides
History
Text
Wolfram Research (2012), FARIMAProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/FARIMAProcess.html.
CMS
Wolfram Language. 2012. "FARIMAProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FARIMAProcess.html.
APA
Wolfram Language. (2012). FARIMAProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FARIMAProcess.html
BibTeX
@misc{reference.wolfram_2025_farimaprocess, author="Wolfram Research", title="{FARIMAProcess}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/FARIMAProcess.html}", note=[Accessed: 20-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_farimaprocess, organization={Wolfram Research}, title={FARIMAProcess}, year={2012}, url={https://reference.wolfram.com/language/ref/FARIMAProcess.html}, note=[Accessed: 20-January-2026]}