MatrixSymbol

MatrixSymbol[a]

represents a matrix with name a.

MatrixSymbol[a,{m,n}]

represents an mn matrix.

MatrixSymbol[a,{m,n},dom]

represents a matrix with elements in the domain dom.

MatrixSymbol[a,{m,n},dom, sym]

represents a matrix with the symmetry sym.

Details

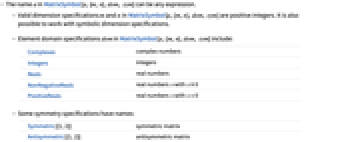
The name a in MatrixSymbol[a,{m,n},dom, sym] can be any expression.
Valid dimension specifications m and n in MatrixSymbol[a,{m,n},dom, sym] are positive integers. It is also possible to work with symbolic dimension specifications.
Element domain specifications dom in MatrixSymbol[a,{m,n},dom, sym] include:

	Complexes	complex numbers
	Integers	integers
	Reals	real numbers
	NonNegativeReals	real numbers x with x≥0
	PositiveReals	real numbers x with x>0

Some symmetry specifications have names:
Symmetric[{1,2}] symmetric matrix

Antisymmetric[{1,2}] antisymmetric matrix
In arithmetic and many other functions that work with lists, MatrixSymbol objects do not automatically combine with other list arguments.
Optimization functions, equation solvers and D recognize that MatrixSymbol objects represent vector variables.

Examples

open allclose all

Basic Examples (1)

Assign the value of the variable a to represent an mn matrix with name "a":

Arithmetic operations recognize that a is not a scalar:

D recognizes that a is a matrix variable:

Scope (5)

Compute derivatives with respect to a matrix variable:

Compute derivatives involving matrix-valued functions:

This requires a real-valued matrix:

Use a matrix variable in optimization:

Solve equations and inequalities involving a matrix variable:

Applications (4)

Approximate the determinant of a perturbed matrix:

Order zero approximation:

Compare with the exact value:

Order one approximation:

Compare with the exact value:

Order two approximation:

Compare with the exact value:

Derive a least-squares solution for data given as a list of pairs :

Find the vector of vertical deviations for the data:

Define the sum of squares of the vertical deviations for the data:

Set up the least-squares equations:

Generate some data:

Solve the least-squares problem for this data:

Find an optimality condition for a portfolio optimization problem with the expected return and standard deviation :

The goal is to maximize when the vector of asset weights satisfies Total[x]=1. The constraint can be used to represent where the unconstrained vector variable consists of the first coordinates of :

The maximum occurs at a critical point of :

Express the condition in terms of :

Compute the gradient of the log-likelihood function of the linear regression model represented by the equation , where are normally distributed random variables with mean zero and variance :