ArraySymbol
ArraySymbol[a]
represents an array with name a.
ArraySymbol[a,{n1,n2,…}]
represents an n1×n2×… array.
ArraySymbol[a,{n1,n2,…},dom]
represents an array with elements in the domain dom.
ArraySymbol[a,{n1,n2,…},dom, sym]
represents an array with the symmetry sym.
Details
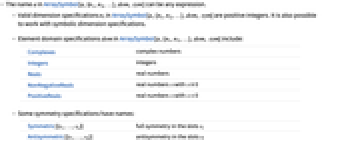
- The name a in ArraySymbol[a,{n1,n2,…},dom, sym] can be any expression.
- Valid dimension specifications ni in ArraySymbol[a,{n1,n2,…},dom, sym] are positive integers. It is also possible to work with symbolic dimension specifications.
- Element domain specifications dom in ArraySymbol[a,{n1,n2,…},dom, sym] include:
-
Complexes complex numbers Integers integers Reals real numbers NonNegativeReals real numbers x with x≥0 PositiveReals real numbers x with x>0 - Some symmetry specifications have names:
-
Symmetric[{s1,…,sn}] full symmetry in the slots si Antisymmetric[{s1,…,sn}] antisymmetry in the slots si - In arithmetic and many other functions that work with lists, ArraySymbol objects do not automatically combine with other list arguments.
- Optimization functions, equation solvers and D recognize that ArraySymbol objects represent vector variables.
Examples
open allclose allBasic Examples (1)
Assign the value of the variable a to represent an mnp array with name "a":
Arithmetic operations recognize that a is not a scalar:
D recognizes that a is an array variable:
Scope (4)
Applications (3)
Derive a least-squares solution for data 
given as a list of pairs 
:
Find the vector of vertical deviations 
for the data:
Define the sum of squares of the vertical deviations for the data:
Set up the least-squares equations:
Solve the least-squares problem for this data:
Find an optimality condition for a portfolio optimization problem with the expected return 
and standard deviation 
:
The goal is to maximize 
when the vector 
of asset weights satisfies Total[x]=1. The constraint can be used to represent 
where the unconstrained vector variable 
consists of the first 
coordinates of 
:
The maximum occurs at a critical point of 
:
Express the condition in terms of 
:
Compute the gradient of the log-likelihood function of the linear regression model represented by the equation 
, where 
are normally distributed random variables with mean zero and variance 
:
The log-likelihood function 
is given by:
Text
Wolfram Research (2024), ArraySymbol, Wolfram Language function, https://reference.wolfram.com/language/ref/ArraySymbol.html.
CMS
Wolfram Language. 2024. "ArraySymbol." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ArraySymbol.html.
APA
Wolfram Language. (2024). ArraySymbol. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArraySymbol.html