ArrayDot

ArrayDot[a,b,k]

computes the product of arrays a and b obtained by summing up products of terms over the last k dimensions of a and the first k dimensions of b.

ArrayDot[a,b,{{s1,t1},{s2,t2},…}]

computes the product of arrays a and b obtained by summing up products of terms over the pairs {si,ti} of dimensions.

Details

  • The arguments a and b in ArrayDot[a,b,k] should be arrays with dimensions, respectively, {m1,…,mp,d1,…,dk} and {d1,…,dk,n1,…,nq}. The result is an array c with dimensions {m1,…,mp,n1,…,nq} and ci1,…,ip,j1,…,jq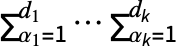sum_(alpha_(1)=1)^(d_(1))...sum_(alpha_k=1)^(d_k)ai1,…,ip,α1,…,αkbα1,…,αk,j1,…,jq.
  • In ArrayDot[a,b,{{s1,t1},…,{sk,tk}}], the arguments a and b should be arrays with dimensions, respectively, {m1,…,mp} and {n1,…,nq}, where all si are distinct, all ti are distinct and for all i, 1≤si≤p, 1≤ti≤q and msinti. The result is equal to TensorContract[ab,{{s1,p+t1},…,{sk,p+tk}}].
  • ArrayDot can be used on SparseArray and structured array objects.
  • ArrayDot is used in the array differentiation chain rule.

Examples

open allclose all

Basic Examples  (3)

Compute ArrayDot over two dimensions:

Compute ArrayDot over specified pairs of dimensions:

ArrayDot is used in the array differentiation chain rule:

Scope  (9)

Exact number arrays:

Real machine-number arrays:

Complex arrays:

Symbolic arrays:

Finite field element arrays:

CenteredInterval arrays:

Find random representatives arep and brep of a and b:

Verify that ArrayDot[a,b,3] contains ArrayDot[arep,brep,3]:

ArrayDot of sparse arrays is another sparse array:

Format the result:

Structured arrays:

Efficiently multiply large arrays:

Applications  (1)

Approximate the determinant of a perturbed matrix:

Order zero approximation:

Compare with the exact value:

Order one approximation:

Compare with the exact value:

Order two approximation:

Compare with the exact value:

Properties & Relations  (9)

ArrayDot is linear in each argument:

Dot[a,b] is equal to ArrayDot[a,b,1]:

SymbolicIdentityArray objects are identity elements for ArrayDot:

For a real matrix a, Norm[a,"Frobenius"] is equal to the square root of ArrayDot[a,a,2]:

If c=ArrayDot[a,b, k], then ci1,…,ip,j1,…,jqsum_(alpha_(1)=1)^(d_(1))...sum_(alpha_k=1)^(d_k)ai1,…,ip,α1,…,αkbα1,…,αk,j1,…,jq:

ArrayDepth[ArrayDot[a,b,k]] is equal to ArrayDepth[a]+ArrayDepth[b]-2k:

ArrayDot can be implemented as a combination of TensorProduct and TensorContract:

ArrayDot can be implemented as a combination of Flatten and Dot:

ArrayDot is used in the array differentiation chain rule:

Wolfram Research (2024), ArrayDot, Wolfram Language function, https://reference.wolfram.com/language/ref/ArrayDot.html.

Text

Wolfram Research (2024), ArrayDot, Wolfram Language function, https://reference.wolfram.com/language/ref/ArrayDot.html.

CMS

Wolfram Language. 2024. "ArrayDot." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ArrayDot.html.

APA

Wolfram Language. (2024). ArrayDot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArrayDot.html

BibTeX

@misc{reference.wolfram_2024_arraydot, author="Wolfram Research", title="{ArrayDot}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/ArrayDot.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_arraydot, organization={Wolfram Research}, title={ArrayDot}, year={2024}, url={https://reference.wolfram.com/language/ref/ArrayDot.html}, note=[Accessed: 21-November-2024 ]}