Inner
Details
- Inner[f,{{a,b},{c,d}},{x,y},g]->{g[f[a,x],f[b,y]],g[f[c,x],f[d,y]]}.
- Like Dot, Inner effectively contracts the last index of the first tensor with the first index of the second tensor. Applying Inner to a rank r tensor and a rank s tensor gives a rank
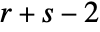 tensor.
tensor. - Inner[f,list1,list2] uses Plus for g. »
- Inner[f,list1,list2,g,n] contracts index n of the first tensor with the first index of the second tensor. »
- The heads of list1 and list2 must be the same, but need not necessarily be List. »
Examples
open all close allBasic Examples (3)
Scope (4)
Generalized inner product of two matrices:
Inner product of a matrix with a vector:
Inner product of a vector with a matrix:
Hermitian inner product of two vectors:
Check this is the same as using Dot and conjugating the second vector:
Generalizations & Extensions (2)
Applications (4)
Tech Notes
Related Guides
Related Links
History
Introduced in 1988 (1.0)
Text
Wolfram Research (1988), Inner, Wolfram Language function, https://reference.wolfram.com/language/ref/Inner.html.
CMS
Wolfram Language. 1988. "Inner." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Inner.html.
APA
Wolfram Language. (1988). Inner. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Inner.html
BibTeX
@misc{reference.wolfram_2025_inner, author="Wolfram Research", title="{Inner}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Inner.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_inner, organization={Wolfram Research}, title={Inner}, year={1988}, url={https://reference.wolfram.com/language/ref/Inner.html}, note=[Accessed: 03-March-2026]}

