Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Wolfram Language & System Documentation Center

DependentVariables

DependentVariables

DependentVariables

is an option for NDSolve and other functions that specifies the list of all objects that should be considered as dependent variables in equations that have been supplied.

Details

With DependentVariables->Automatic, the dependent variables are determined from the equations.
DependentVariables->{u₁,u₂,…} specifies a complete list of dependent variables u_i representing functions that should be solved for, even if the solutions are not eventually returned.
DependentVariables->{uspec₁,uspec₂,…} can be used to specify ranges for dependent variables.
Possible forms for uspec_i are:

	u	u has range Reals or Complexes
	Element[u,Reals]	u has range Reals
	Element[u,Complexes]	u has range Complexes
	Element[u,{v₁,…}]	u has discrete range {v₁,…}
	{u,u_min,u_max}	u has range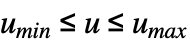
	uspec_iaction_i	perform action_i when uspec_i is no longer satisfied

Examples

open all close all

Basic Examples (2)

Save only the solution for x[t]:

Plot the solution x[t] as a function of t:

Stop the integration when the solution has left a specified range:

Scope (4)

Multiple range specifications can be enforced for a single dependent variable:

Perform a custom action when a dependent variable goes out of range:

The event action each time the variable leaves the specified range:

Print a message and stop the integration the first time a variable goes out of range:

Applications (2)

Set up a very large system of equations:

Solve for all of the dependent variables, but save only the solution for x₁:

This saves a lot of memory versus saving all the solutions:

Model an unstable inverted pendulum with oscillating base:

Stop the simulation if θ[t] goes outside the range :

At a stable amplitude, the inverted pendulum with oscillating base will not fall out of range:

Properties & Relations (1)

Variable range checking can also be achieved with WhenEvent:

An equivalent range check with DependentVariables is more direct and comprehensible:

WhenEvent is useful for more complicated range checking:

Possible Issues (3)

A variable cannot be specified as both dependent and discrete:

A dependent variable cannot have a discrete range:

The variables in a range specification must be valid dependent variables:

Use conditions directly for the dependent variable:

Or use a WhenEvent expression in the equation:

Top