LerchPhi[z,s,a]
gives the Lerch transcendent ![]() .
.


LerchPhi
LerchPhi[z,s,a]
gives the Lerch transcendent ![]() .
.
Details and Options

- Mathematical function, suitable for both symbolic and numerical manipulation.
- LerchPhi is a generalization of Zeta[s], Zeta[s,a], PolyLog and related functions. »
- For
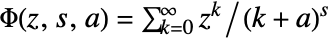 , the Lerch transcendent is defined by
, the Lerch transcendent is defined by ![TemplateBox[{z, s, a}, LerchPhi]=sum_(k=0)^(infty)(z^k)/((k+a)^s) TemplateBox[{z, s, a}, LerchPhi]=sum_(k=0)^(infty)(z^k)/((k+a)^s)](Files/LerchPhi.en/3.png) .
. - For
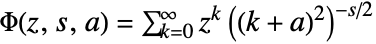 , the definition used is
, the definition used is ![TemplateBox[{z, s, a}, LerchPhi]=sum_(k=0)^(infty)(z^k)/(((k+a)^2)^(s/2)) TemplateBox[{z, s, a}, LerchPhi]=sum_(k=0)^(infty)(z^k)/(((k+a)^2)^(s/2))](Files/LerchPhi.en/5.png) , where by default any term with
, where by default any term with 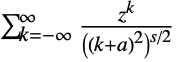 is excluded.
is excluded. - LerchPhi is identical to HurwitzLerchPhi for
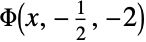 . »
. » - LerchPhi follows the branch cut conventions of the generalized Riemann
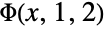 function as given by Zeta. By contrast, HurwitzLerchPhi uses the branch cuts as defined by HurwitzZeta. »
function as given by Zeta. By contrast, HurwitzLerchPhi uses the branch cuts as defined by HurwitzZeta. » - Unlike HurwitzLerchPhi, LerchPhi by default has regularized, finite values when the defining series has terms with zero denominator. »
- LerchPhi takes the following options:
-
DoublyInfinite False whether to compute the transcendent defined by a doubly inifinite sum IncludeSingularTerm False whether to include terms for which 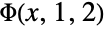
- LerchPhi[z,s,a,DoublyInfinite->True] gives the sum
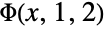 .
. - The option IncludeSingularTermFalse only affects values at
![a in TemplateBox[{}, NonPositiveIntegers] a in TemplateBox[{}, NonPositiveIntegers]](Files/LerchPhi.en/11.png) and
and 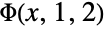 . »
. » - For certain special arguments, LerchPhi automatically evaluates to exact values.
- LerchPhi can be evaluated to arbitrary numerical precision.
- LerchPhi automatically threads over lists.
- LerchPhi can be used with Interval and CenteredInterval objects. »
Examples
open all close allBasic Examples (6)
Simple exact values are generated automatically:
Plot over a subset of the reals:
Plot over a subset of the complexes:
Series expansion at the origin:
Series expansion at Infinity:
Scope (32)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix LerchPhi function using MatrixFunction:
Specific Values (6)
Simple exact values are generated automatically:
![]() is a rational function in
is a rational function in ![]() and a polynomial in
and a polynomial in ![]() if
if ![]() :
:
The following is manifestly a rational function in ![]() :
:
LerchPhi[z,s,0] is simply PolyLog[s,z]:
LerchPhi[z,s,1] is PolyLog[s,z]/z:
LerchPhi[-1,s,a] gives expressions in Zeta:
Approaching along the line ![]() gives the same result:
gives the same result:
Approaching along the line ![]() gives
gives ![]() :
:
Approaching the origin along the line ![]() also gives 1, but in a more interesting fashion:
also gives 1, but in a more interesting fashion:
Find a value of z for which LerchPhi[z,1,0]=1.05:
Visualization (3)
Plot the LerchPhi function:
Plot the real part of the LerchPhi function:
Plot the imaginary part of the LerchPhi function:
Visualize how LerchPhi and HurwitzLerchPhi agree for ![]() but not
but not ![]() :
:
Function Properties (11)
Real domain of LerchPhi:
Approximate function range of ![]() :
:
LerchPhi threads elementwise over lists and matrices:
![]() is neither non-decreasing nor non-increasing:
is neither non-decreasing nor non-increasing:
![]() is neither non-negative nor non-positive:
is neither non-negative nor non-positive:
![]() has both singularity and discontinuity for
has both singularity and discontinuity for ![]() or for
or for ![]() :
:
![]() is neither convex nor concave:
is neither convex nor concave:
TraditionalForm formatting:
Differentiation (2)
Series Expansions (4)
Find the Taylor expansion in ![]() for generic
for generic ![]() and
and ![]() using Series:
using Series:
Plots of the first three approximations around ![]() :
:
Series expansion in ![]() at a generic point:
at a generic point:
Series expansion about ![]() when
when ![]() has the singular value
has the singular value ![]() and
and ![]() :
:
Do the expansion about ![]() instead:
instead:
Series expansion in ![]() near
near ![]() ,
, ![]() ,
, ![]() :
:
Series expansion in ![]() about the same point:
about the same point:
LerchPhi can be applied to power series:
Options (5)
DoublyInfinite (3)
IncludeSingularTerm (2)
LerchPhi by default gives regularized, finite values for ![]() for
for ![]() :
:
Obtain the raw, infinite value by setting IncludeSingularTerm->True:
For noninteger ![]() , the option does not change the value:
, the option does not change the value:
Nor does it have any effect when ![]() :
:
LerchPhi[z,s,a,IncludeSingularTermTrue] is ComplexInfinity when there is a singular term and ![]() :
:
Applications (2)
Find a zero of LerchPhi:
Properties & Relations (10)
Obtain LerchPhi from sums:
LerchPhi is a numeric function:
LerchPhi[z,s,a] gives regularized, finite values when a:
HurwitzLerchPhi agrees with LerchPhi for ![]() :
:
LerchPhi by default omits singular terms for which the denominator is zero:
The term ![]() in the defining series is omitted:
in the defining series is omitted:
HurwitzLerchPhi, by contrast, includes these terms:
Zeta[s] equals LerchPhi[1,s,1] for Re[s]>1:
Zeta[s,a] equals LerchPhi[1,s,a] for Re[s]>1:
HurwitzLerchPhi is different from LerchPhi in the choice of branch cuts:
HurwitzLerchPhi matches HurwitzZeta, while LerchPhi matches Zeta:
LerchPhi is a generalization of PolyLog:
DirichletEta is a special case of LerchPhi:
DirichletBeta is dilation of LerchPhi:
Possible Issues (4)
A larger setting for $MaxExtraPrecision can be needed:
LerchPhi uses numerical comparisons when singular terms are included:
For ![]() , LerchPhi cannot always be evaluated in terms of Zeta for symbolic s:
, LerchPhi cannot always be evaluated in terms of Zeta for symbolic s:
The line ![]() is not considered to have a singular term:
is not considered to have a singular term:
This is consistent with Sum, which considers ![]() to be
to be ![]() for all
for all ![]() :
:
See Also
Zeta PolyLog HurwitzLerchPhi DirichletEta DirichletBeta
Function Repository: ArcTanIntegral
Tech Notes
Related Links
History
Introduced in 1988 (1.0) | Updated in 2023 (13.3)
Text
Wolfram Research (1988), LerchPhi, Wolfram Language function, https://reference.wolfram.com/language/ref/LerchPhi.html (updated 2023).
CMS
Wolfram Language. 1988. "LerchPhi." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/LerchPhi.html.
APA
Wolfram Language. (1988). LerchPhi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LerchPhi.html
BibTeX
@misc{reference.wolfram_2025_lerchphi, author="Wolfram Research", title="{LerchPhi}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/LerchPhi.html}", note=[Accessed: 02-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_lerchphi, organization={Wolfram Research}, title={LerchPhi}, year={2023}, url={https://reference.wolfram.com/language/ref/LerchPhi.html}, note=[Accessed: 02-March-2026]}