GoldenRatio

GoldenRatio

is the golden ratio , with numerical value .

Details

  • Mathematical constant treated as numeric by NumericQ and as a constant by D.
  • GoldenRatio can be evaluated to any numerical precision using N.

Background & Context

  • GoldenRatio is the symbol representing the golden ratio 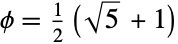, a constant that gives the limiting value of the ratios of successive Fibonacci numbers lim_(n->infty) (TemplateBox[{n}, Fibonacci])/(TemplateBox[{{n, -, 1}}, Fibonacci]) as well as the value of the "simplest" possible continued fraction 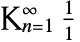. It has a numerical value 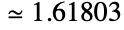. GoldenRatio arises in many mathematical computations including sums, recurrence relations, continued fractions, nested radicals, special trigonometric values, and the ratios of side lengths for simple geometric figures such as the pentagon, pentagram, and dodecahedron. GoldenRatio is also related to a number of naturally occurring phenomena, as well as with the logarithmic spiral.
  • When GoldenRatio is used as a symbol, it is propagated as an exact quantity that can be expressed in terms of radicals using FunctionExpand. Expansion and simplification of complicated expressions involving GoldenRatio may require use of functions such as FunctionExpand and FullSimplify.
  • Based on its algebraic definition, GoldenRatio is irrational (meaning it cannot be expressed as a ratio of any two integers) but algebraic (meaning it is the root of an integer polynomial—in this case 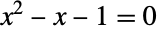). While it is not known if GoldenRatio is normal (meaning the digits in its base- expansion are equally distributed) to any base, its known digits are very uniformly distributed.
  • GoldenRatio can be evaluated to arbitrary numerical precision using N. In fact, calculating the first million decimal digits of GoldenRatio takes only a fraction of a second on a modern desktop computer. RealDigits can be used to return a list of digits of GoldenRatio and ContinuedFraction to obtain terms of its continued fraction expansion.

Examples

open allclose all

Basic Examples  (1)

Numerical value:

Scope  (4)

Evaluate to any precision:

Do exact computations:

Simplify GoldenRatio expressions:

TraditionalForm formatting:

Applications  (7)

Golden ratio rectangle:

Make a phyllotaxis pattern ("simulated sunflower head"):

Compute the Fibonacci numbers:

Corners of an icosahedron:

Position of 1s in a Fibonacci substitution system [more info]:

Compute the effective "inverse" of the Fibonacci numbers:

Properties & Relations  (3)

Neat Examples  (1)

Simulated palm tree trunk:

Wolfram Research (1988), GoldenRatio, Wolfram Language function, https://reference.wolfram.com/language/ref/GoldenRatio.html.

Text

Wolfram Research (1988), GoldenRatio, Wolfram Language function, https://reference.wolfram.com/language/ref/GoldenRatio.html.

CMS

Wolfram Language. 1988. "GoldenRatio." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GoldenRatio.html.

APA

Wolfram Language. (1988). GoldenRatio. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GoldenRatio.html

BibTeX

@misc{reference.wolfram_2024_goldenratio, author="Wolfram Research", title="{GoldenRatio}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/GoldenRatio.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_goldenratio, organization={Wolfram Research}, title={GoldenRatio}, year={1988}, url={https://reference.wolfram.com/language/ref/GoldenRatio.html}, note=[Accessed: 21-November-2024 ]}