Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

EllipticTheta

EllipticTheta[a,u,q]

gives the theta function .

EllipticTheta[a,q]

gives the theta constant .

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
$TemplateBox[{1, u, q}, EllipticTheta]=2q^(1/4)sum_(n=0)^(infty)(-1)^nq^(n(n+1))sin((2 n+1)u)$ .
$TemplateBox[{2, u, q}, EllipticTheta]=2q^(1/4)sum_(n=0)^(infty)q^(n(n+1))cos((2 n+1)u)$ .
$TemplateBox[{3, u, q}, EllipticTheta]=1+2sum_(n=1)^(infty)q^(n^2)cos(2n u)$ .
$TemplateBox[{4, u, q}, EllipticTheta]=1+2sum_(n=1)^(infty)(-1)^nq^(n^2)cos(2n u)$ .
The 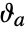are only defined within the unit q disk, ; the unit disk forms a natural boundary of analyticity.
Within the unit q disk, 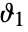and have branch cuts from 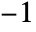to .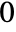
For certain special arguments, EllipticTheta automatically evaluates to exact values.
EllipticTheta can be evaluated to arbitrary numerical precision.
EllipticTheta automatically threads over lists.
EllipticTheta can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples (3)

Evaluate numerically:

Plot over a subset of the reals:

Series expansion at the origin with respect to q:

Scope (20)

Numerical Evaluation (5)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

EllipticTheta can be used with Interval and CenteredInterval objects:

Specific Values (3)

Value at zero:

EllipticTheta evaluates symbolically for special arguments:

Find the first positive minimum of EllipticTheta[3,x,1/2]:

Visualization (2)

Plot the EllipticTheta function for various parameters:

Plot the real part of :

Plot the imaginary part of :

Function Properties (10)

Real and complex domains of EllipticTheta:

EllipticTheta is a periodic function with respect to :

EllipticTheta threads elementwise over lists:

is an analytic function of x:

For example, has no singularities or discontinuities:

is neither nondecreasing nor nonincreasing:

is not injective:

is not surjective:

is neither non-negative nor non-positive:

is neither convex nor concave:

TraditionalForm formatting:

Generalizations & Extensions (1)

EllipticTheta can be applied to a power series:

Applications (11)

Plot theta functions near the unit circle in the complex q plane:

The number of representations of as a sum of four squares:

Verify Jacobi's triple product identity through a series expansion:

Conformal map from an ellipse to the unit disk:

Visualize the map:

Green's function for the 1D heat equation with Dirichlet boundary conditions and initial condition :

Plot the time‐dependent temperature distribution:

Form Bloch functions of a one‐dimensional crystal with Gaussian orbitals:

Plot Bloch functions as a function of the quasi‐wave vector:

Electrostatic potential in a NaCl‐like crystal with point-like ions:

Plot the potential in a plane through the crystal:

A concise form of the Poisson summation formula:

An asymptotic approximation for a finite Gaussian sum:

Compare the approximate and exact values for :

Closed form of iterates of the arithmetic‐geometric mean:

Compare the closed form with explicit iterations:

Form any elliptic function with given periods, poles and zeros as a rational function of EllipticTheta:

Form an elliptic function with a single and a double zero and a triple pole:

Plot the resulting elliptic function:

Properties & Relations (2)

Numerically find a root of a transcendental equation:

Sum can generate elliptic theta functions:

Possible Issues (4)

Machine-precision input is insufficient to give a correct answer:

Use arbitrary-precision arithmetic to obtain the correct result:

The first argument must be an explicit integer between 1 and 4:

EllipticTheta has the attribute NHoldFirst:

Different argument conventions exist for theta functions:

Neat Examples (1)

Visualize a function with a boundary of analyticity:

Top