SiegelTheta[Ω,s]
gives the Siegel theta function ![]() with Riemann modular matrix Ω and vector s.
with Riemann modular matrix Ω and vector s.
SiegelTheta[{ν1,ν2},Ω,s]
gives the Siegel theta function ![]() with characteristics ν1 and ν2.
with characteristics ν1 and ν2.


SiegelTheta
SiegelTheta[Ω,s]
gives the Siegel theta function ![]() with Riemann modular matrix Ω and vector s.
with Riemann modular matrix Ω and vector s.
SiegelTheta[{ν1,ν2},Ω,s]
gives the Siegel theta function ![]() with characteristics ν1 and ν2.
with characteristics ν1 and ν2.
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
- The matrix Ω must be symmetric, with positive definite imaginary part.
- If Ω is a p×p matrix, the vectors s and v or νi must have length p.
-
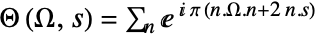 , where n ranges over all possible vectors in the p-dimensional integer lattice.
, where n ranges over all possible vectors in the p-dimensional integer lattice. -
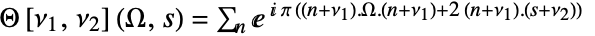 , where n ranges over all possible vectors in the p-dimensional integer lattice.
, where n ranges over all possible vectors in the p-dimensional integer lattice. - SiegelTheta can be evaluated to arbitrary numerical precision.
Examples
open all close allBasic Examples (3)
Scope (7)
Numerical Evaluation (3)
Specific Values (2)
Visualization (2)
Plot the SiegelTheta function for various parameters:
Generalizations & Extensions (2)
SiegelTheta with characteristics ![]() and
and ![]() :
:
SiegelTheta with characteristics simplifies symbolically for special arguments:
Applications (2)
Plot of the absolute value of SiegelTheta in the complex plane:
Properties & Relations (2)
In one dimension, SiegelTheta coincides with the EllipticTheta functions:
SiegelTheta satisfies the equations:
Possible Issues (2)
SiegelTheta requires a symmetric ![]() matrix:
matrix:
Machine precision may be insufficient to obtain a correct answer:
Neat Examples (1)
Visualize deviations from positivity in nested SiegelTheta functions:
See Also
Related Guides
Related Links
History
Text
Wolfram Research (2007), SiegelTheta, Wolfram Language function, https://reference.wolfram.com/language/ref/SiegelTheta.html.
CMS
Wolfram Language. 2007. "SiegelTheta." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SiegelTheta.html.
APA
Wolfram Language. (2007). SiegelTheta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SiegelTheta.html
BibTeX
@misc{reference.wolfram_2025_siegeltheta, author="Wolfram Research", title="{SiegelTheta}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/SiegelTheta.html}", note=[Accessed: 05-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_siegeltheta, organization={Wolfram Research}, title={SiegelTheta}, year={2007}, url={https://reference.wolfram.com/language/ref/SiegelTheta.html}, note=[Accessed: 05-March-2026]}