ExponentialGeneratingFunction[expr,n,x]
gives the exponential generating function in x for the sequence whose n![]() term is given by the expression expr.
term is given by the expression expr.
ExponentialGeneratingFunction[expr,{n1,n2,…},{x1,x2,…}]
gives the multidimensional exponential generating function in x1, x2, … whose n1, n2, … term is given by expr.


ExponentialGeneratingFunction
ExponentialGeneratingFunction[expr,n,x]
gives the exponential generating function in x for the sequence whose n![]() term is given by the expression expr.
term is given by the expression expr.
ExponentialGeneratingFunction[expr,{n1,n2,…},{x1,x2,…}]
gives the multidimensional exponential generating function in x1, x2, … whose n1, n2, … term is given by expr.
Details and Options
- The exponential generating function for a sequence whose
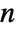
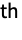 term is
term is 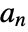 is given by
is given by 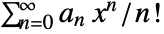 .
. - The multidimensional exponential generating function is given by
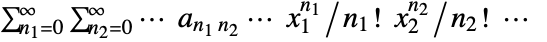 .
. - The following options can be given:
-
Assumptions $Assumptions assumptions to make about parameters GenerateConditions False whether to generate answers that involve conditions on parameters Method Automatic method to use VerifyConvergence True whether to verify convergence
Examples
open all close allBasic Examples (1)
Scope (19)
Basic Uses (6)
Exponential generating function of a univariate sequence:
Exponential generating function of a multivariate sequence:
Compute a typical exponential generating function:
Plot the magnitude using Plot3D, ContourPlot or DensityPlot:
Generate conditions for the region of convergence:
Evaluate the exponential generating function at a point:
Plot both the spectrum and the plot phase using color:
Plot the spectrum in the complex plane using ParametricPlot3D:
ExponentialGeneratingFunction will use several properties including linearity:
Multiplication by exponentials:
Multiplication by polynomials:
ExponentialGeneratingFunction automatically threads over lists:
Special Sequences (13)
Factorial exponential polynomials:
Trigonometric, exponential and polynomial:
Combinations of the previous input:
Different ways of expressing piecewise-defined signals:
Rational exponential functions:
Hypergeometric term sequences:
The DiscreteRatio is rational for all hypergeometric term sequences:
Many functions give hypergeometric terms:
Any products are hypergeometric terms:
Transforms of hypergeometric terms:
A holonomic sequence is defined by a linear difference equation:
Many special function are holonomic sequences in their index:
DifferenceRoot in general results in DifferentialRoot functions:
Options (5)
GenerateConditions (1)
By default, no conditions are given for where a generating function is convergent:
Use GenerateConditions to generate conditions of validity:
VerifyConvergence (3)
Setting VerifyConvergence to False will treat generating functions as formal objects:
Setting VerifyConvergence to True will verify that the radius of convergence is nonzero:
In addition, setting GenerateConditions to True will display the conditions for convergence:
Properties & Relations (3)
ExponentialGeneratingFunction effectively computes an infinite sum:
ExponentialGeneratingFunction is closely related to GeneratingFunction:
Possible Issues (1)
A ExponentialGeneratingFunction may not converge for all values of parameters:
Use GenerateConditions to get the region of convergence:
Related Guides
History
Text
Wolfram Research (2008), ExponentialGeneratingFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/ExponentialGeneratingFunction.html.
CMS
Wolfram Language. 2008. "ExponentialGeneratingFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ExponentialGeneratingFunction.html.
APA
Wolfram Language. (2008). ExponentialGeneratingFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ExponentialGeneratingFunction.html
BibTeX
@misc{reference.wolfram_2025_exponentialgeneratingfunction, author="Wolfram Research", title="{ExponentialGeneratingFunction}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/ExponentialGeneratingFunction.html}", note=[Accessed: 16-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_exponentialgeneratingfunction, organization={Wolfram Research}, title={ExponentialGeneratingFunction}, year={2008}, url={https://reference.wolfram.com/language/ref/ExponentialGeneratingFunction.html}, note=[Accessed: 16-January-2026]}