



ArcTan
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- All results are given in radians.
- For real
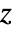 , the results are always in the range
, the results are always in the range 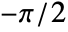 to
to 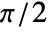 .
. - For certain special arguments, ArcTan automatically evaluates to exact values.
- ArcTan can be evaluated to arbitrary numerical precision.
- ArcTan automatically threads over lists.
- ArcTan[z] has branch cut discontinuities in the complex
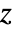 plane running from
plane running from 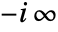 to
to 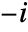 and
and 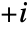 to
to 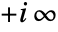 .
. - If
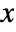 or
or 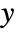 is complex, then ArcTan[x,y] gives
is complex, then ArcTan[x,y] gives 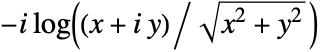 . When
. When 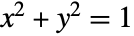 , ArcTan[x,y] gives the number
, ArcTan[x,y] gives the number 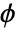 such that
such that 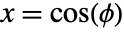 and
and 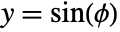 .
. - ArcTan can be used with Interval and CenteredInterval objects. »
Background & Context
- ArcTan is the inverse tangent function. For a real number x, ArcTan[x] represents the radian angle measure
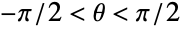 such that
such that 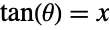 . The two-argument form ArcTan[x,y] represents the arc tangent of y/x, taking into account the quadrant in which the point
. The two-argument form ArcTan[x,y] represents the arc tangent of y/x, taking into account the quadrant in which the point 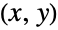 lies. It therefore gives the angular position (expressed in radians) of the point measured from the positive
lies. It therefore gives the angular position (expressed in radians) of the point measured from the positive 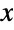 axis. ArcTan is consequently useful when converting from Cartesian to polar coordinate systems and for finding the phase
axis. ArcTan is consequently useful when converting from Cartesian to polar coordinate systems and for finding the phase 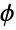 in phasor notation
in phasor notation ![x+ⅈ y=TemplateBox[{z}, Abs]ⅇ^(ⅈ phi) x+ⅈ y=TemplateBox[{z}, Abs]ⅇ^(ⅈ phi)](Files/ArcTan.en/25.png) .
. - ArcTan automatically threads over lists. For certain special exact arguments, ArcTan automatically evaluates to exact values. When given exact numeric expressions as arguments, ArcTan may be evaluated to arbitrary numeric precision. Operations useful for manipulation of symbolic expressions involving ArcTan include FunctionExpand, TrigToExp, TrigExpand, Simplify, and FullSimplify.
- ArcTan is defined for complex argument
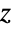 via
via 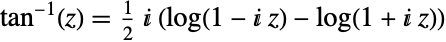 . ArcTan[z] has branch cut discontinuities in the complex
. ArcTan[z] has branch cut discontinuities in the complex 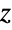 plane.
plane. - Related mathematical functions include Arg, Tan, ArcCot, ArcTanh, and Gudermannian.
Examples
open all close allBasic Examples (7)
Scope (49)
Numerical Evaluation (6)
Evaluate using the two-argument form:
The precision of the output tracks the precision of the input:
Evaluate for complex arguments:
The two-argument form supports complex numbers:
Evaluate ArcTan efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix ArcTan function using MatrixFunction:
Specific Values (6)
Visualization (4)
Function Properties (12)
ArcTan is defined for all real values:
ArcTan achieves all real values from the interval ![]() :
:
Function range for arguments from the complex domain:
ArcTan is an odd function:
ArcTan has the mirror property ![]() :
:
![]() is an analytic function of
is an analytic function of ![]() over the reals:
over the reals:
It is neither analytic nor meromorphic over the complex plane:
![]() is not analytic over the reals:
is not analytic over the reals:
ArcTan is injective:
ArcTan is not surjective:
ArcTan is neither non-negative nor non-positive:
![]() has no singularities or discontinuities:
has no singularities or discontinuities:
ArcTan is neither convex nor concave:
TraditionalForm formatting:
Integration (3)
Series Expansions (4)
Integral Transforms (3)
Function Identities and Simplifications (3)
Function Representations (5)
Represent using ArcCot:
Representation through inverse Jacobi functions:
Represent using Hypergeometric2F1:
ArcTan can be represented in terms of MeijerG:
ArcTan can be represented as a DifferentialRoot:
Applications (9)
Find angles of the right triangle with sides 3, 4 and hypotenuse 5:
Find integrals of rational functions in terms of ArcTan:
Addition theorem for tangent function:
Find the slope angle of the line through a pair of points ![]() and
and ![]() :
:
Solve a differential equation:
Branch cuts of ArcTan run along the imaginary axis:
Polar decomposition of a complex number:
Special solution of the sine–Gordon equation:
The cumulative distribution function (CDF) of the standard distribution of the hyperbolic secant is given in terms of ArcTan:
This is a scaled and shifted version of the Gudermannian function:
Properties & Relations (5)
Use TrigToExp to express ArcTan using Log:
Use FullSimplify to simplify expressions with ArcTan:
ArcTan gives the angle in radians, while ArcTanDegrees gives the same angle in degrees:
ArcTan is a special case of some special functions:
Possible Issues (1)
Because ArcTan is a multivalued function, ![]()
See Also
Arg Tan ArcCot ArcTanDegrees ArcTanh Degree TrigToExp TrigExpand Gudermannian
Function Repository: ArcTanDegree
Tech Notes
History
Introduced in 1988 (1.0) | Updated in 2021 (13.0)
Text
Wolfram Research (1988), ArcTan, Wolfram Language function, https://reference.wolfram.com/language/ref/ArcTan.html (updated 2021).
CMS
Wolfram Language. 1988. "ArcTan." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ArcTan.html.
APA
Wolfram Language. (1988). ArcTan. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArcTan.html
BibTeX
@misc{reference.wolfram_2025_arctan, author="Wolfram Research", title="{ArcTan}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/ArcTan.html}", note=[Accessed: 03-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_arctan, organization={Wolfram Research}, title={ArcTan}, year={2021}, url={https://reference.wolfram.com/language/ref/ArcTan.html}, note=[Accessed: 03-January-2026]}