Reduce

Reduce[expr,vars]

reduces the statement expr by solving equations or inequalities for vars and eliminating quantifiers.

Reduce[expr,vars,dom]

does the reduction over the domain dom. Common choices of dom are Reals, Integers, and Complexes.

Details and Options

  • The statement expr can be any logical combination of:
  • lhs==rhsequations
    lhs!=rhsinequations
    lhs>rhs or lhs>=rhs inequalities
    expr∈domdomain specifications
    {x,y,…}∈regregion specification
    ForAll[x,cond,expr]universal quantifiers
    Exists[x,cond,expr]existential quantifiers
  • The result of Reduce[expr,vars] always describes exactly the same mathematical set as expr.
  • Reduce[{expr1,expr2,…},vars] is equivalent to Reduce[expr1&&expr2&&…,vars].
  • Reduce[expr,vars] assumes by default that quantities appearing algebraically in inequalities are real, while all other quantities are complex.
  • Reduce[expr,vars,dom] restricts all variables and parameters to belong to the domain dom.
  • If dom is Reals, or a subset such as Integers or Rationals, then all constants and function values are also restricted to be real.
  • Reduce[expr&&vars∈Reals,vars,Complexes] performs reductions with variables assumed real, but function values allowed to be complex.
  • Reduce[expr,vars,Integers] reduces Diophantine equations over the integers.
  • Reduce[…,x∈reg,Reals] constrains x to be in the region reg. The different coordinates for x can be referred to using Indexed[x,i].
  • Reduce[expr,{x1,x2,…},…] effectively writes expr as a combination of conditions on x1, x2, … where each condition involves only the earlier .
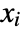  • Algebraic variables in expr free of the 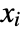and of each other are treated as independent parameters.
  • Applying LogicalExpand to the results of Reduce[expr,…] yields an expression of the form 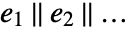, where each of the 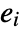can be thought of as representing a separate component in the set defined by expr.
  • The 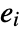may not be disjoint and may have different dimensions. After LogicalExpand, each of the 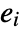has the form .
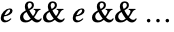  • Without LogicalExpand, Reduce by default returns a nested collection of conditions on the 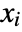, combined alternately by Or and And on successive levels.
  • When expr involves only polynomial equations and inequalities over real or complex domains, then Reduce can always in principle solve directly for all the .
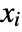  • When expr involves transcendental conditions or integer domains, Reduce will often introduce additional parameters in its results.
  • When expr involves only polynomial conditions, Reduce[expr,vars,Reals] gives a cylindrical algebraic decomposition of expr.
  • Reduce can give explicit representations for solutions to all linear equations and inequalities over the integers and can solve a large fraction of Diophantine equations described in the literature.
  • When expr involves only polynomial conditions over real or complex domains, Reduce[expr,vars] will always eliminate quantifiers, so that quantified variables do not appear in the result.
  • The following options can be given:
  • Backsubstitution Falsewhether to give results unwound by backsubstitution »
    Cubics Falsewhether to use explicit radicals to solve all cubics »
    GeneratedParameters Chow to name parameters that are generated »
    Modulus 0modulus to assume for integers »
    Quartics Falsewhether to use explicit radicals to solve all quartics »
  • Reduce[expr,{x1,x2,…},Backsubstitution->True] yields a form in which values from equations generated for earlier 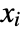are backsubstituted so that the conditions for a particular 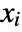have only minimal dependence on earlier . »

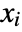Examples

open allclose all

Basic Examples  (4)

Reduce equations and inequalities:

Use specific domains:

Reduce a quantified expression:

Reduce with geometric region constraints:

Scope  (83)

Basic Uses  (5)

Find an explicit description of the solution set of a system of equations:

Use ToRules and ReplaceRepeated (//.) to list the solutions:

Find an explicit description of the solution set of a system of inequalities:

Find solutions over specified domains:

The solution set may depend on symbolic parameters:

Representing solutions may require introduction of new parameters:

List the first 10 solutions:

Complex Domain  (16)

A linear system:

A univariate polynomial equation:

A multivariate polynomial equation:

Systems of polynomial equations and inequations can always be reduced:

A quantified polynomial system:

An algebraic system:

Transcendental equations solvable in terms of inverse functions:

In this case there is no solution:

Equations involving elliptic functions:

Equations solvable using special function zeros:

Solving this system does not require the Riemann hypothesis:

Elementary function equation in a bounded region:

Holomorphic function equation in a bounded region:

Here Reduce finds some solutions but is not able to prove there are no other solutions:

Equation with a purely imaginary period over a vertical stripe in the complex plane:

Doubly periodic transcendental equation:

A system of transcendental equations solvable using inverse functions:

A square system of analytic equations over a bounded box:

Real Domain  (26)

A linear system:

A univariate polynomial equation:

A univariate polynomial inequality:

A multivariate polynomial equation:

A multivariate polynomial inequality:

Systems of polynomial equations and inequalities can always be reduced:

A quantified polynomial system:

An algebraic system:

Piecewise equations:

Piecewise inequalities:

Transcendental equations, solvable using inverse functions:

Transcendental inequalities, solvable using inverse functions:

Inequalities involving elliptic functions:

Transcendental equation, solvable using special function zeros:

Transcendental inequality, solvable using special function zeros:

Exp-log equations:

High-degree sparse polynomial equation:

Algebraic equation involving high-degree radicals:

Equation involving irrational real powers:

Exp-log inequality:

Elementary function equation in a bounded interval:

Holomorphic function equation in a bounded interval:

Meromorphic function inequality in a bounded interval:

Periodic elementary function equation over the reals:

Transcendental systems solvable using inverse functions:

Systems exp-log in the first variable and polynomial in the other variables:

Quantified system:

Systems elementary and bounded in the first variable and polynomial in the other variables:

Quantified system:

Systems analytic and bounded in the first variable and polynomial in the other variables:

Quantified system:

Square systems of analytic equations over bounded regions:

Integer Domain  (13)

Linear system of equations:

A linear system of equations and inequalities:

A univariate polynomial equation:

A univariate polynomial inequality:

Binary quadratic equations:

A Thue equation:

A sum of squares equation:

The Pythagorean equation:

A bounded system of equations and inequalities:

A high-degree system with no solution:

Transcendental Diophantine systems:

A polynomial system of congruences:

Diophantine equations with irrational coefficients:

Modular Domains  (5)

A linear system:

A univariate polynomial equation:

A multivariate polynomial equation:

A system of polynomial equations and inequations:

Reduce a quantified polynomial system:

Finite Field Domains  (4)

Univariate equations:

Systems of linear equations:

Systems of polynomial equations:

Systems involving quantifiers:

Mixed Domains  (4)

Mixed real and complex variables:

Find real values of and complex values of for which is real and less than :

Reduce an inequality involving Abs[x]:

Plot the solution set:

Mixed integer and real variables:

Geometric Regions  (10)

Constrain variables to basic geometric regions in 2D:

Plot the solution:

Constrain variables to basic geometric regions in 3D:

Plot the solution:

Project a 3D region onto the - plane:

Plot the projection:

An implicitly defined region:

A parametrically defined region:

Derived regions:

The solution of restricted to the intersection:

Eliminate quantifiers over a Cartesian product of regions:

Regions dependent on parameters:

A condition for :

Use to specify that is a vector in :

In this case is a vector in :

Options  (6)

Backsubstitution  (1)

Since y appears after x in the variable list, Reduce may use x to express the solution for y:

With Backsubstitution->True, Reduce gives explicit numeric values for y:

Cubics  (1)

By default, Reduce does not use general formulas for solving cubics in radicals:

With Cubics->True, Reduce solves all cubics in terms of radicals:

GeneratedParameters  (1)

Reduce may introduce new parameters to represent the solution:

Use GeneratedParameters to control how the parameters are generated:

Modulus  (1)

Solve equations over the integers modulo 9:

Quartics  (1)

By default, Reduce does not use general formulas for solving quartics in radicals:

With Quartics->True, Reduce solves all quartics in terms of radicals:

WorkingPrecision  (1)

Finding the solution with exact computations takes a long time:

With WorkingPrecision->100, Reduce finds a solution fast, but it may be incorrect:

Applications  (9)

Basic Applications  (1)

Prove geometric inequalities for , , and sides of a triangle:

Prove an inequality for triangles:

Prove an inequality for acute triangles:

Polynomial Root Problems  (1)

Find conditions for a quartic to have all roots equal:

Using quantifier elimination:

Using Subresultants:

Parametrization Problems  (1)

Plot a space curve given by an implicit description:

Plot the projection of the space curve on the - plane:

Integer Problems  (3)

Find a Pythagorean triple:

Find a sequence of Pythagorean triples:

Find how to pay $2.27 postage with 10-, 23- and 37-cent stamps:

The same task can be accomplished with IntegerPartitions:

Show that there are only five regular polyhedrons:

Each face for a regular -gon contributes edges, but they are shared, so they are counted twice:

Each face for a regular -gon contributes vertices, but they are shared, so they are counted times:

Using Euler's formula , find the number of faces:

For this last formula to be well defined, the denominator needs to be positive and an integer:

Hence the following five cases:

Compare this to the actual counts in PolyhedronData:

Geometry Problems  (3)

The region ℛ is a subset of if is true. Show that Disk[{0,0},{2,1}] is a subset of Rectangle[{-2,-1},{2,1}]:

Plot it:

Show that Cylinder[]⊆Ball[{0,0,0},2]:

Plot it:

For a finite point set , the Voronoi cell for a point can be defined by , which corresponds to all points closer to than any other point for . Find a simple formula for a Voronoi cell, using Reduce:

The Voronoi cell associated with pts〚1〛 is given by:

The resulting cell is given by an intersection of half-spaces:

Find simple formulas for all Voronoi cells:

Plot them:

Properties & Relations  (10)

The result of reduction is equivalent to the original system:

ToRules and ReplaceRepeated can be used to backsubstitute finite solution sets:

Use Expand to simplify a result of substitution involving simple radicals:

To simplify expressions involving algebraic numbers,, use RootReduce:

To find solution instances, use FindInstance:

Solve represents solutions of complex equations in terms of replacement rules:

Solve omits solutions involving equations on parameters:

For transcendental equations, Solve may not give all solutions:

Using inverse functions allows Solve to find some solutions fast:

Finding the complete solution may take much longer, and the solution may be large:

This finds the values of for which x 2 is a solution:

SolveAlways gives the values of parameters for which complex equations are always true:

This solves the same problem using Reduce:

Resolve eliminates quantifiers, possibly without solving the resulting quantifier‐free system:

Eliminate eliminates variables from systems of complex equations:

This solves the same problem using Resolve:

Reduce additionally solves the resulting equations:

Possible Issues  (3)

Because appears in an inequality, it is assumed to be real; is allowed to be complex:

When domain Reals is specified, , , and Sqrt[x] are required to be real:

This allows complex values of for which both sides of the inequality are real:

Reduce does not solve equations that depend on branch cuts of Wolfram Language functions:

Plot the region where the first condition is nonzero:

Removable singularities of input equations are generally not considered valid solutions:

However, solutions may include removable singularities that are cancelled by automatic simplification:

The removable singularity at is cancelled by evaluation:

Here the removable singularity at is cancelled by Together, which is used to preprocess the equation:

Neat Examples  (1)

Find the vertical asymptotes of by directly using the definition of limit:

Wolfram Research (1988), Reduce, Wolfram Language function, https://reference.wolfram.com/language/ref/Reduce.html (updated 2024).

Text

Wolfram Research (1988), Reduce, Wolfram Language function, https://reference.wolfram.com/language/ref/Reduce.html (updated 2024).

CMS

Wolfram Language. 1988. "Reduce." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Reduce.html.

APA

Wolfram Language. (1988). Reduce. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Reduce.html

BibTeX

@misc{reference.wolfram_2025_reduce, author="Wolfram Research", title="{Reduce}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Reduce.html}", note=[Accessed: 24-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_reduce, organization={Wolfram Research}, title={Reduce}, year={2024}, url={https://reference.wolfram.com/language/ref/Reduce.html}, note=[Accessed: 24-April-2025 ]}