CylindricalDecomposition[expr,{x1,x2,…}]
finds a decomposition of the region represented by the statement expr into cylindrical parts whose directions correspond to the successive xi.
CylindricalDecomposition[expr,{x1,x2,…},op]
finds a decomposition of the result of applying the topological operation op to the region represented by the statement expr.
CylindricalDecomposition[expr,{x1,x2,…},"Function"]
represents the result as CylindricalDecompositionFunction[…][x1,x2,…] that can be efficiently used in further computation.


CylindricalDecomposition
CylindricalDecomposition[expr,{x1,x2,…}]
finds a decomposition of the region represented by the statement expr into cylindrical parts whose directions correspond to the successive xi.
CylindricalDecomposition[expr,{x1,x2,…},op]
finds a decomposition of the result of applying the topological operation op to the region represented by the statement expr.
CylindricalDecomposition[expr,{x1,x2,…},"Function"]
represents the result as CylindricalDecompositionFunction[…][x1,x2,…] that can be efficiently used in further computation.
Details and Options



- The statement expr can be any logical combination of:
-
lhs==rhs equations lhs!=rhs inequations lhs>rhs or lhs>=rhs inequalities CylindricalDecompositionFunction[…][x,y,…] cylindrical algebraic formulas ForAll[x,cond,expr] universal quantifiers Exists[x,cond,expr] existential quantifiers - Equations and inequalities may involve polynomials, rational functions or real algebraic functions.
- CylindricalDecomposition assumes that all variables are real.
- CylindricalDecomposition returns inequalities whose bounds in general involve algebraic functions.
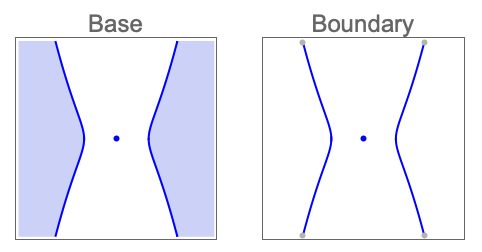
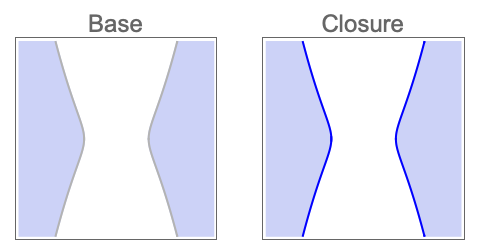
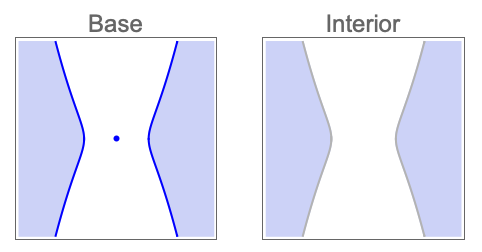
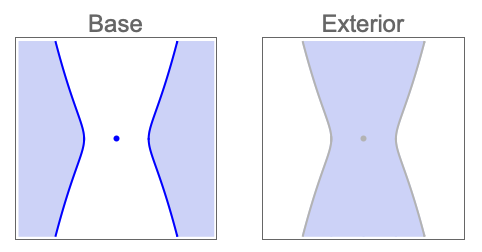
- The topological operation op can be one of:
-
"Boundary" boundary of the solution set "Closure" closure of the solution set "Interior" interior of the solution set "Exterior" exterior of the solution set "ClosureOfInterior" closure of the interior of the solution set "InteriorOfClosure" interior of the closure of the solution set "Components" connected components of the solution set - CylindricalDecompositionFunction objects provide an explicit compact representation of semialgebraic sets that can be efficiently used in further computation.
- CylindricalDecompositionFunction objects are typically used for repeated computations with semialgebraic sets, including computing Boolean combinations of sets, restricting sets with additional conditions, eliminating some variables or optimizing over sets.
- A cylindrical algebraic formula in x1,…,xn has the form
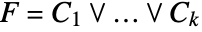 , where
, where 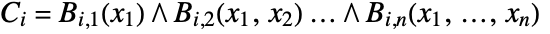 . Each
. Each 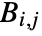 has the form either
has the form either 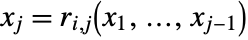 or
or 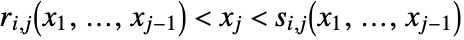 , where
, where 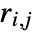 and
and 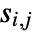 are algebraic functions that are defined and continuous on the solution set of
are algebraic functions that are defined and continuous on the solution set of 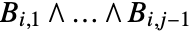 . The solution set
. The solution set 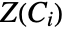 of
of 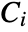 in
in 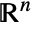 is called a cell. Projections of cells
is called a cell. Projections of cells 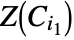 and
and 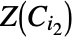 on
on 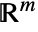 , for any
, for any 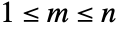 , are either disjoint or identical.
, are either disjoint or identical. - Without the "Function" specification, CylindricalDecomposition returns cylindrical algebraic formulas written explicitly as Boolean combinations of equations and inequalities.
- CylindricalDecompositionFunction provides an encapsulated representation of cylindrical algebraic formulas, which is often more efficient when used in the input to CylindricalDecomposition or to solvers such as Reduce, Resolve, FindInstance, Solve or Minimize.
- Normal converts CylindricalDecompositionFunction objects to explicit Boolean combinations of equations and inequalities.
- Specifications of topological operations and output format can be combined, e.g. CylindricalDecomposition[ineqs,{x1,x2,…},"BoundaryFunction"] gives the boundary of the solution set of ineqs represented as a CylindricalDecompositionFunction object.
Examples
open all close allBasic Examples (2)
Scope (14)
Basic Uses (9)
For univariate polynomials, the result consists of intervals:
In general, individual points can occur:
This is the form for any logical combination as well:
For multivariate polynomials, the result is in cylinder form ![]() :
:
In general, several cylinders will result:
Plot the individual cylinders using RegionPlot:
By changing the order of variables, the cylinders take the form ![]() :
:
Plot the individual cylinders:
Here cylinders of dimensions 0, 2, and 1 occur in the result:
Three- and four-dimensional decompositions:
CylindricalDecomposition allows quantified formulas:
Coefficients can include real algebraic numbers:
Topological Operations (5)
Find decompositions of the solution region and its boundary:
Find decompositions of the solution region and its closure:
Find decompositions of the solution region and its interior:
Find decompositions of the solution region and its exterior:
Find decompositions of the solution region and its connected components:
Options (1)
WorkingPrecision (1)
This computation takes a long time due to high degrees of numeric coefficients:
This finds a decomposition using WorkingPrecision->1000, but the result may be incorrect:
Applications (2)
Properties & Relations (8)
Use RegionPlot to visualize 2D semialgebraic sets:
Use RegionPlot3D to visualize 3D semialgebraic sets:
Resolve performs quantifier elimination and may avoid computing cylindrical decomposition:
Reduce in addition deals with different domains and transcendental functions:
Use FindInstance to find points that satisfy equations and inequalities:
SemialgebraicComponentInstances will give sample points in each cylinder:
CylindricalDecomposition merges several cylinders to get a more compact representation:
GenericCylindricalDecomposition will compute the full-dimensional part only:
Possible Issues (2)
CylindricalDecomposition requires exact, infinite‐precision input:
Rationalize will convert inexact numbers to exact ones:
In general, the output can be in a nested and more compact form:
Flatten the result into disjunctive normal form without splitting the inequalities:
Related Guides
History
Introduced in 2003 (5.0) | Updated in 2017 (11.2) ▪ 2020 (12.2)
Text
Wolfram Research (2003), CylindricalDecomposition, Wolfram Language function, https://reference.wolfram.com/language/ref/CylindricalDecomposition.html (updated 2020).
CMS
Wolfram Language. 2003. "CylindricalDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/CylindricalDecomposition.html.
APA
Wolfram Language. (2003). CylindricalDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CylindricalDecomposition.html
BibTeX
@misc{reference.wolfram_2025_cylindricaldecomposition, author="Wolfram Research", title="{CylindricalDecomposition}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CylindricalDecomposition.html}", note=[Accessed: 20-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_cylindricaldecomposition, organization={Wolfram Research}, title={CylindricalDecomposition}, year={2020}, url={https://reference.wolfram.com/language/ref/CylindricalDecomposition.html}, note=[Accessed: 20-January-2026]}