Minimize

Minimize[f,x]

minimizes f symbolically with respect to x.

Minimize[f,{x,y,…}]

minimizes f symbolically with respect to x, y, ….

Minimize[{f,cons},{x,y,…}]

minimizes f symbolically subject to the constraints cons.

Minimize[…,x∈rdom]

constrains x to be in the region or domain rdom.

Minimize[…,…,dom]

constrains variables to the domain dom, typically Reals or Integers.

Details and Options

  • Minimize is also known as infimum, symbolic optimization and global optimization (GO).
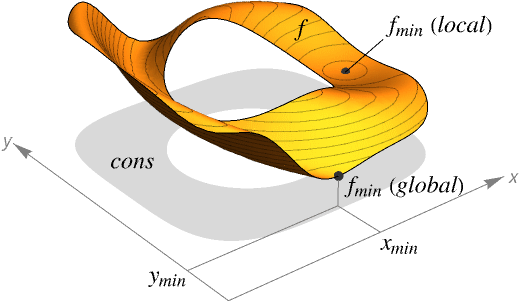
  • Minimize finds the global minimum of f subject to the constraints given.
  • Minimize is typically used to find the smallest possible values given constraints. In different areas, this may be called the best strategy, best fit, best configuration and so on.
  • Minimize returns a list of the form {fmin,{x->xmin,y->ymin,…}}.
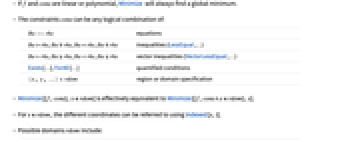
  • If f and cons are linear or polynomial, Minimize will always find a global minimum.
  • The constraints cons can be any logical combination of:
  • lhs==rhsequations
    lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhsinequalities (LessEqual,…)
    lhsrhs, lhsrhs, lhsrhs, lhsrhsvector inequalities (VectorLessEqual,…)
    Exists[…], ForAll[…]quantified conditions
    {x,y,…}∈rdomregion or domain specification
  • Minimize[{f,cons},x∈rdom] is effectively equivalent to Minimize[{f,cons∧x∈rdom},x].
  • For x∈rdom, the different coordinates can be referred to using Indexed[x,i].
  • Possible domains rdom include:
  • Realsreal scalar variable
    Integersinteger scalar variable
    Vectors[n,dom]vector variable in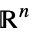
    Matrices[{m,n},dom]matrix variable in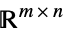
    ℛvector variable restricted to the geometric region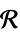
  • By default, all variables are assumed to be real.
  • Minimize will return exact results if given exact input. With approximate input, it automatically calls NMinimize.
  • Minimize will return the following forms:
  • {fmin,{xxmin,…}}finite minimum
    {∞,{xIndeterminate,…}}infeasible, i.e. the constraint set is empty
    {-∞,{xxmin,…}}unbounded, i.e. the values of f can be arbitrarily small
  • If the minimum is achieved only infinitesimally outside the region defined by the constraints, or only asymptotically, Minimize will return the infimum and the closest specifiable point.
  • Even if the same minimum is achieved at several points, only one is returned.
  • N[Minimize[…]] calls NMinimize for optimization problems that cannot be solved symbolically.
  • Minimize[f,x,WorkingPrecision->n] uses n digits of precision while computing a result. »

Examples

open allclose all

Basic Examples  (5)

Minimize a univariate function:

Minimize a multivariate function:

Minimize a function subject to constraints:

A minimization problem containing parameters:

Minimize a function over a geometric region:

Plot it:

Scope  (36)

Basic Uses  (7)

Minimize over the unconstrained reals:

Minimize subject to constraints :

Constraints may involve arbitrary logical combinations:

An unbounded problem:

An infeasible problem:

The infimum value may not be attained:

Use a vector variable and a vector inequality:

Univariate Problems  (7)

Unconstrained univariate polynomial minimization:

Constrained univariate polynomial minimization:

Exp-log functions:

Analytic functions over bounded constraints:

Periodic functions:

Combination of trigonometric functions with commensurable periods:

Combination of periodic functions with incommensurable periods:

Piecewise functions:

Unconstrained problems solvable using function property information:

Multivariate Problems  (9)

Multivariate linear constrained minimization:

Linear-fractional constrained minimization:

Unconstrained polynomial minimization:

Constrained polynomial optimization can always be solved:

The minimum value may not be attained:

The objective function may be unbounded:

There may be no points satisfying the constraints:

Quantified polynomial constraints:

Algebraic minimization:

Bounded transcendental minimization:

Piecewise minimization:

Convex minimization:

Minimize convex objective function such that is positive semidefinite and :

Plot the region and the minimizing point:

Parametric Problems  (4)

Parametric linear optimization:

The minimum value is a continuous function of parameters:

Parametric quadratic optimization:

The minimum value is a continuous function of parameters:

Unconstrained parametric polynomial minimization:

Constrained parametric polynomial minimization:

Optimization over Integers  (3)

Univariate problems:

Integer linear programming:

Polynomial minimization over the integers:

Optimization over Regions  (6)

Minimize over a region:

Plot it:

Find the minimum distance between two regions:

Plot it:

Find the minimum such that the triangle and ellipse still intersect:

Plot it:

Find the disk of minimum radius that contains the given three points:

Plot it:

Using Circumsphere gives the same result directly:

Use to specify that is a vector in :

Find the minimum distance between two regions:

Plot it:

Options  (1)

WorkingPrecision  (1)

Finding the exact solution takes a long time:

With WorkingPrecision->100, you get an exact minimum value, but it might be incorrect:

Applications  (10)

Basic Applications  (3)

Find the minimal perimeter among rectangles with a unit area:

Find the minimal perimeter among triangles with a unit area:

The minimal perimeter triangle is equilateral:

Find the distance to a parabola from a point on its axis:

Assuming a particular relationship between the and parameters:

Geometric Distances  (6)

The shortest distance of a point in a region ℛ to a given point p and a point q realizing the shortest distance is given by Minimize[EuclideanDistance[p,q],q∈ℛ]. Find the shortest distance and the nearest point to {1,1} in the unit Disk[]:

Plot it:

Find the shortest distance and the nearest point to {1,3/4} in the standard unit simplex Simplex[2]:

Plot it:

Find the shortest distance and the nearest point to {1,1,1} in the standard unit sphere Sphere[]:

Plot it:

Find the shortest distance and the nearest point to {-1/3,1/3,1/3} in the standard unit simplex Simplex[3]:

Plot it:

The nearest points p∈ and q∈ and their distance can be found through Minimize[EuclideanDistance[p,q],{p∈,q∈}]. Find the nearest points in Disk[{0,0}] and Rectangle[{3,3}] and the distance between them:

Plot it:

Find the nearest points in Line[{{0,0,0},{1,1,1}}] and Ball[{5,5,0},1] and the distance between them:

Plot it:

Geometric Centers  (1)

If ℛ⊆n is a region that is full dimensional, then the Chebyshev center is the center of the largest inscribed ball of ℛ. The center and the radius of the largest inscribed ball of ℛ can be found through Minimize[SignedRegionDistance[ℛ,p], p∈ℛ]. Find the Chebyshev center and the radius of the largest inscribed ball for Rectangle[]:

Find the Chebyshev center and the radius of the largest inscribed ball for Triangle[]:

Properties & Relations  (6)

Minimize gives an exact global minimum of the objective function:

NMinimize attempts to find a global minimum numerically, but may find a local minimum:

FindMinimum finds local minima depending on the starting point:

The minimum point satisfies the constraints, unless messages say otherwise:

The given point minimizes the distance from the point {2,}:

When the minimum is not attained, Minimize may give a point on the boundary:

Here the objective function tends to the minimum value when y tends to infinity:

Minimize can solve linear programming problems:

LinearProgramming can be used to solve the same problem given in matrix notation:

This computes the minimum value:

Use RegionDistance and RegionNearest to compute the distance and the nearest point:

Both can be computed using Minimize:

Use RegionBounds to compute the bounding box:

Use Maximize and Minimize to compute the same bounds:

Possible Issues  (1)

Minimize requires that all functions present in the input be real-valued:

Values for which the equation is satisfied but the square roots are not real are disallowed:

Wolfram Research (2003), Minimize, Wolfram Language function, https://reference.wolfram.com/language/ref/Minimize.html (updated 2021).

Text

Wolfram Research (2003), Minimize, Wolfram Language function, https://reference.wolfram.com/language/ref/Minimize.html (updated 2021).

CMS

Wolfram Language. 2003. "Minimize." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Minimize.html.

APA

Wolfram Language. (2003). Minimize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Minimize.html

BibTeX

@misc{reference.wolfram_2025_minimize, author="Wolfram Research", title="{Minimize}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Minimize.html}", note=[Accessed: 28-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_minimize, organization={Wolfram Research}, title={Minimize}, year={2021}, url={https://reference.wolfram.com/language/ref/Minimize.html}, note=[Accessed: 28-July-2025 ]}